
Moses Boudourides and Gerasimos Antypas (2002) 'A Simulation of the Structure of the World-Wide Web'
Sociological Research Online, vol. 7, no. 1, <http://www.socresonline.org.uk/7/1/boudourides.html>
To cite articles published in Sociological Research Online, please reference the above information and include paragraph numbers if necessary
Received: 9/8/2001 Accepted: 7/5/2002 Published: 31/5/2002
 Abstract
Abstract Introduction
Introduction Discussion of the Simulation
Discussion of the Simulation
 Description of the Simulation
Description of the Simulation
X' = X + (Xlnk - X)(1 - m)/2,where m is a value between zero and one, which increases randomly but monotonically for each successive link.
 Results
Results
| Parameter | Description | Value |
| a | Probability threshold to introduce new web sites | 0.2 |
| ß | Probability threshold to introduce new topics | 0.5 |
| y | Probability threshold to increase the number of new web pages | 0.0025 |
| T | Total number of topics | 200 |
| p1 | Probability threshold to introduce a link with a page of the same topic | 0.5 |
| p2 | Probability threshold to introduce a link with a page of a different topic | 0.0005 |
|
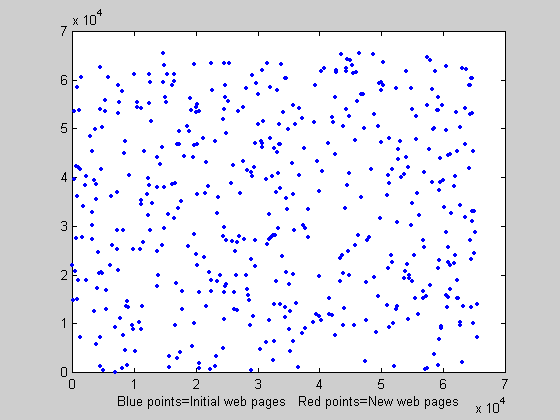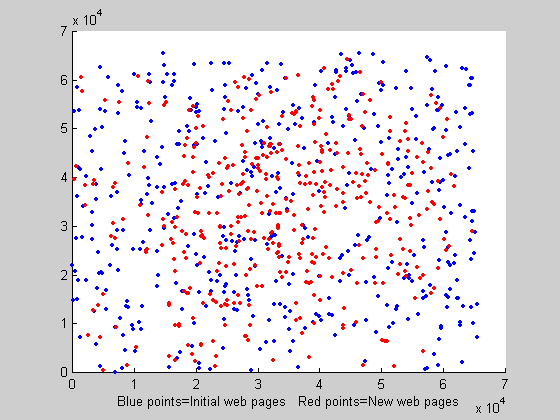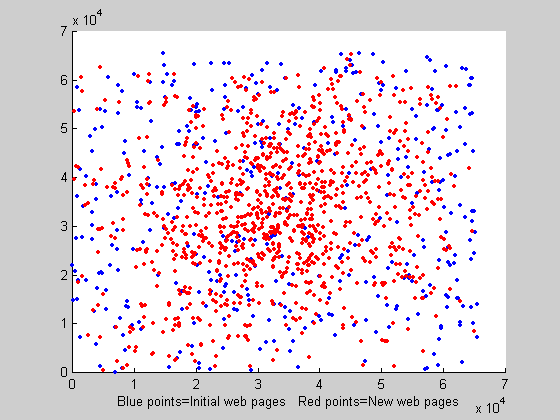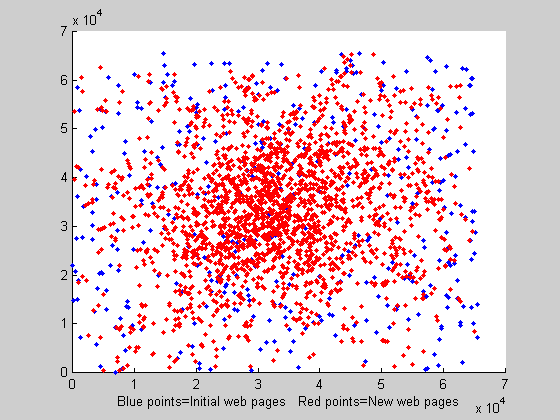
| Animation 1. Web pages generation every 25 time units |
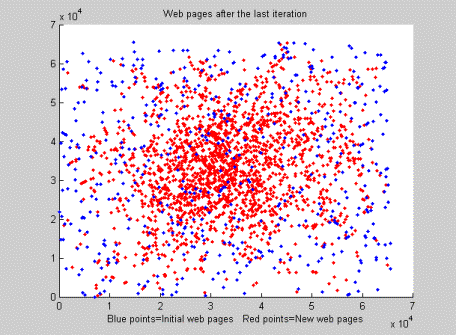
|
| Figure 1: The simulation output |
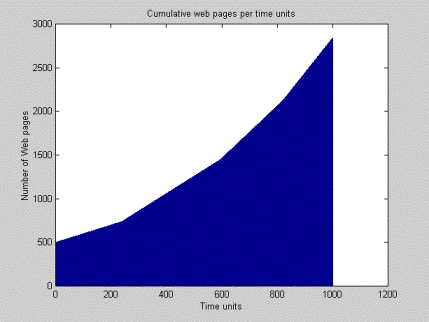
|
| Figure 2: Cumulative web pages per time unit |
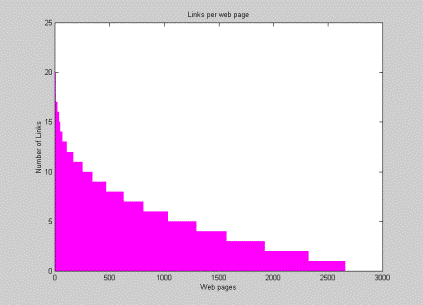
|
| Figure 3: Out-going links per web page |
|
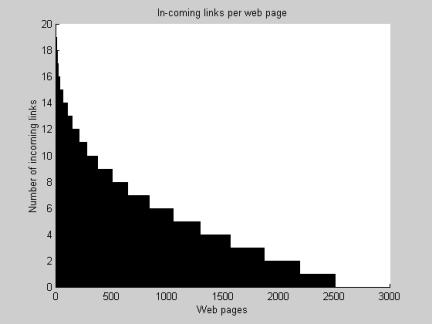
| Figure 4: In-coming links per web page |
|
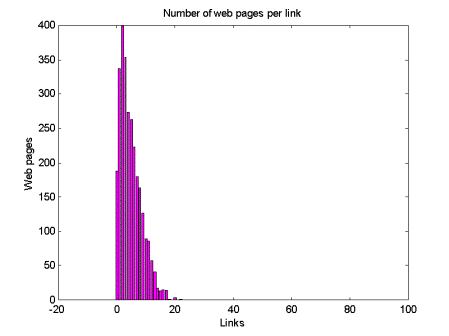
| Figure 5: Links per web page |
|
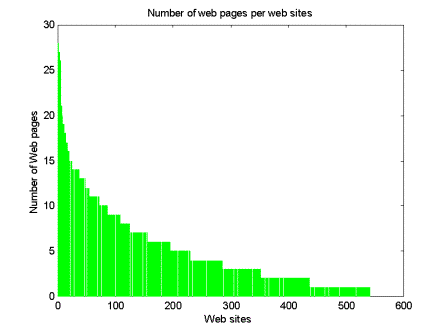
| Figure 6 Web pages per web site |
| Number of Web Pages | Simulation | Distribution |
| 1 | 105 | 106 |
| 2 | 85 | 83 |
| 3 | 66 | 66 |
| 4 | 56 | 53 |
| 5 | 34 | 43 |
| 6 | 40 | 35 |
| 7 | 31 | 29 |
| 8 | 16 | 23 |
| 9 | 23 | 19 |
| 10 | 13 | 16 |
| 11 | 18 | 13 |
| 12 | 7 | 16 |
| 13 | 10 | 13 |
| 14 | 13 | 10 |
| 15 | 5 | 9 |
| 16 | 3 | 7 |
| 17 | 3 | 6 |
| 18 or more | 13 | 19 |
pn = an-ke-n/g,where a, k, g are the parameters. In our simulation, we have used a least square optimisation in order to evaluate these parameters and we have found them to take the following values:
a = 128.4421
k = 0.0783
g = 5.1872
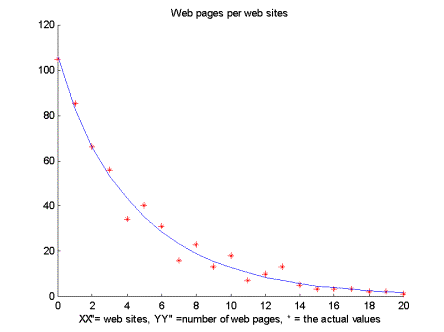
|
| Figure 7: Web pages per web site |
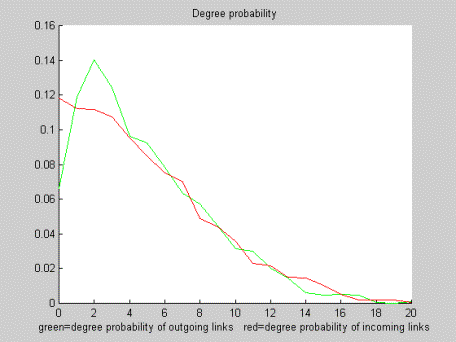
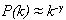 at large k. Indeed, Barabási & Albert found that y = 2.45 for out-going links and y = 2.1 for in-coming links, a result that was confirmed in a parallel study by Ravi Kumar and co-workers (Kumar 1999). In the present simulation, we have computed that y = 2.3637 for out-going links and y = 2.3641 for in-coming links, which verifies that our simulation produces a scale-free network such as the real World-Wide Web.[11]
at large k. Indeed, Barabási & Albert found that y = 2.45 for out-going links and y = 2.1 for in-coming links, a result that was confirmed in a parallel study by Ravi Kumar and co-workers (Kumar 1999). In the present simulation, we have computed that y = 2.3637 for out-going links and y = 2.3641 for in-coming links, which verifies that our simulation produces a scale-free network such as the real World-Wide Web.[11]
|
| Figure 8: Probability distribution of links |
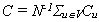 .
.
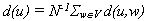 and the average path length d of the graph G is defined as
and the average path length d of the graph G is defined as 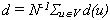 .
.
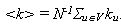 . Now, for a random graph, one easily computes that the clustering coefficient is
. Now, for a random graph, one easily computes that the clustering coefficient is 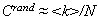 and the average path length is
and the average path length is 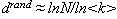 .
.
 Conclusions
Conclusions
 Notes
Notes2The authors wish to thank the referees of the paper for providing useful suggestions on the sociological discussion of the Web.
3This is the initiative of the 'semantic web' currently launched by the World-Wide Web Consortium (W3C). According to Berners-Lee, Handler & Lassila (2001): "The Semantic Web is an extension of the current web in which information is given well-defined meaning, better enabling computers and people to work in cooperation".
4 Unintended or unanticipated consequences (Merton, 1936) are of tremendous interest to sociologists in the tradition of Merton's (1963) discussions of manifest versus latent functions of purposive action. They also play a central role in more recent sociological developments such as Giddens's (1984) structuration theory.
5This is the dogma of the 'Actor Network Theory,' in which the development and stabilisation of scientific and technological objects (facts and artefacts) results from the construction of heterogeneous networks as concrete alignments between human actors, natural phenomena, and social or technical intervening aspects (Callon, 1986; Latour, 1987). However, not everybody would subscribe to these ideas; for some this is a controversial theory and sometimes serious objections are risen against it (Collins, 1994).
6Albert et al. (1999) have estimated the degree of connectivity of the web concluding that any two web pages are separated by an average of '19 clicks.'
7We are tempted to call 'infene' this quantum of information captured by web pages in analogy with Gilbert's neologism.
8 The Matlab program of this simulation is available online at: <http://nicomedia.math.upatras.gr/simulations/ssweb.m>
9 The results of the sensitivity analysis to the variation of the simulation parameters are given in the following table:
| a | ß | y | T | p1 | p2 | Average number of links | Clustering coefficient | Number of pages | Number of sites |
| 0.18 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 6.7681 | 0.1953 | 4019 | 728 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.22 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4,5022 | 0,2029 | 2678 | 609 |
| 0.20 | 0.4 | 0.0025 | 200 | 0.50 | 0.0005 | 2.6180 | 0.2283 | 1500 | 298 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.6 | 0.0025 | 200 | 0.50 | 0.0005 | 4.4691 | 0.2059 | 2528 | 475 |
| 0.20 | 0.5 | 0.0022 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.5 | 0.0028 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.5 | 0.0025 | 180 | 0.50 | 0.0005 | 6.0627 | 0.2010 | 3364 | 694 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.5 | 0.0025 | 250 | 0.50 | 0.0005 | 5.4559 | 0.1761 | 4018 | 822 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.47 | 0.0005 | 2.9335 | 0.2025 | 1653 | 325 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.55 | 0.0005 | 4.3863 | 0.2313 | 2358 | 449 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0003 | 2.9620 | 0.2417 | 1791 | 371 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0005 | 4.8256 | 0.1998 | 2844 | 541 |
| 0.20 | 0.5 | 0.0025 | 200 | 0.50 | 0.0010 | 5.8110 | 0.1525 | 3011 | 596 |
10 Exponentially truncated powers laws have been used by Newman (2000) in a study of scientific co-authorship networks.
11Although it appears as a disparity in our simulation's computation (y = 2.3637 for out-going links and y = 2.3641 for in-coming links) in contrast with what Barabási & Albert (1999) have found (? = 2.45 for out-going links and y = 2.1 for in-coming links), we must stress the fact that our simulation is based on a rather simplistic model of the real Web, while Barabási & Albert have collected information about a large sample of the real Web composed of over 800 million web pages. What is important is that the results of a simple simulation as ours are exhibiting the same structure with that of the real World-Wide Web: the connectivities of the simulated web pages follow too a scale-free power-law distribution.
12 Again the reason that our simulation has resulted a different value of average path length d than what was computed by Albert, Jeong & Barabási (1999) is due to the fact that our simulation was based on a rather simplistic model of the World-Wide Web, while Albert et al. had focused on a very large sample of the real Web. However, it is in both cases the comparison with the corresponding random graph that implies the property of the small-world.
ALBERT, R., and BARABASI, A.-L. (2001). 'Statistical Mechanics of Complex Networks', LANL arXiv:cond-mat/0106096, <http://xxx.lanl.gov/abs/cond-mat/0106096>.
ALBERT, R., JEONG, H., and BARABASI, A.-L. (1999). 'Diameter of the World-Wide Web', Nature, Vol. 401, pp. 130-131.
BARABASI, A.-L., and ALBERT, R. (1999). 'Emergence of scaling in random networks', Science, Vol. 286, pp. 509-511.
BERNERS-LEE, T., HENDLER, J., & LASSILA, O. (2001). 'The Semantic Web', Scientific American, Issue 501, <http://www.sciam.com/2001/0501issue/0501berners-lee.html>.
BHARAT, K, & BRODER, A. (1998). 'A technique for measuring the relative size and overlap of public Web search engines', WWW7/Computer Networks, Vol. 30, No. 1-7, pp. 379-388.
BRAY, T. (1996). 'Measuring the Web', Fifth International World Wide Web Conference, <http://www5conf.inria.fr/fich_html/papers/P9/Overview.html>.
BRODER, A., KUMAR, R., MAGHOULL, F., RAGHAVAN, P., RAJAGOPALAN, S., STATA R., TOMKINS, A. & WIENER, J. (2000). 'Graph structure in the web', Computer Networks, Vol. 33, No. 1-6, pp. 309-320, <http://www.almaden.ibm.com/cs/k53/www9.final>.
CALLON, M. (1986). 'The sociology of an Actor Network' in M. Callon, J. Law & A. Rip (editors) Mapping the Dynamics of Science and Technology. London: Macmillan.
COLLINS, H.M. (1994) 'Bruno Latour: We Have Never Been Modern', Isis, Vol. 85, No. 4, 672-674.
CROWSTON, K., & WILLIAMS, M. (1999). 'The effects of linking on genres of web documents', in Proceedings of the 32nd Annual Hawaii International Conference on System Sciences; Genre in Digital Documents. Los Alamitos CA: IEEE Computer Society, <http://crowston.syr.edu/papers/ddgen04.pdf>.
DRUCKER, S.J., & GUMPERT (eds.) (1999). Real Law at Virtual Space: Communication Regulation in Cyberspace. Cresskill, NJ: Hampton Press.
ERDOS, P., and RENYI, A. (1959). 'On random graphs. I', Publicationes Mathematicae (Debrecen), Vol. 6, pp. 290-297.
GIDDENS, A. (1984). The Constitution of Society: Outline of the Theory of Structuration. Berkeley: University of California Press.
GILBERT, N. (1997). 'A Simulation of the Structure of Academic Science', Sociological Research Online, Vol. 2, No. 2, <http://www.socresonline.org.uk/2/2/3.html>.
HEATH, D., KOCH, E., LEY, B., & MONTOYA, M. (1999). 'Nodes and queries: Linking locations in networked fields of inquiry', American Behavioral Scientist, Vol. 43, pp. 450-463.
HEGSELMANN, R., & FLACHE, A. (1998). 'Understanding complex social dynamics: A plea for cellular automata based modelling', Journal of Artificial Societies and Social Simulation, Vol. 1, No. 3, <http://jasss.soc.surrey.ac.uk/1/3/1.html>.
HOLLAND, J.H. (1998). Emergence: From Chaos to Order. Redwood City, CA: Addison-Wesley.
KUMAR, R., RAGHAVAN, P., RAJAGOPALAN, S., and TOMKINS, A. (1999). 'Trawling the Web for emerging cyber-communities', Computer Networks, Vol. 31, pp. 1481-1493.
LATOUR, B. (1987). Science in Action. Cambridge, MA: Harvard University Press.
MACEY, M. (1998). 'Social order in artificial worlds', Journal of Artificial Societies and Social Simulation, Vol. 1, No. 1, <http://jasss.soc.surrey.ac.uk/1/1/4.html>
MERTON, R.K. (1936). 'The unanticipated consequences of purposive social action', American Sociological Review, Vol. 1. pp. 894-920.
MERTON, R.K. (1963). Social Theory and Social Structure. Glencoe, IL: Free Press.
NEWMAN, M.E.J. (2000). 'Who is the best connected scientist? A study of scientific coauthorship networks', Santa Fe Working Paper 00-12-064, <http://www.santafe.edu/sfi/publications/Abstracts/00-12-064.ps>.
SHEPHERD & WATTERS (1999). 'The functionality attribute of cybergenres', in Proceedings of the 32nd Annual Hawaii International Conference of System Sciences; Genre in Digital Documents. Los Alamitos CA: IEEE Computer Society.
WATTS, D.J. (1999). Small-worlds. Princeton, NJ: Princeton University Press.
WATTS, D.J., and STROGATZ, S.H. (1998). Collective dynamics of 'small-world' networks. Nature, Vol. 393, pp. 440-442.