
Gilbert, N. (1997) 'A Simulation
of the Structure of Academic Science'
Sociological Research
Online, vol. 2, no. 2,
<http://www.socresonline.org.uk/2/2/3.html>
To cite articles published in Sociological Research Online, please reference the above information and include paragraph numbers if necessary
Received: 11/2/97 Accepted: 19/5/97 Published: 30/6/97
 Abstract
AbstractThis paper reports on a simulation designed to see whether it is possible to reproduce the form of these observed relationships using a small number of simple assumptions. The simulation succeeds in generating a specialty structure with 'areas' of science displaying growth and decline. It also reproduces Lotka's Law concerning the distribution of citations among authors.
The simulation suggests that it is possible to generate many of the quantitative features of the present structure of science and that one way of looking at scientific activity is as a system in which scientific papers generate further papers, with authors (scientists) playing a necessary but incidental role. The theoretical implications of these suggestions are briefly explored.
 Introduction
Introduction
 Simulation as a Method
Simulation as a Method
 Artificial Societies
Artificial Societies
 Simulating Lotka's Law
Simulating Lotka's Law
 , that the next author is an author who has not previously published in the
journal. From these two propositions, Simon is able to derive the formula for the Zipf
distribution:
, that the next author is an author who has not previously published in the
journal. From these two propositions, Simon is able to derive the formula for the Zipf
distribution:
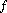 (i) = ai-k
(i) = ai-k
 = p/n
= p/n
 , give the publication a new (i.e.
previously unpublished) author.
, give the publication a new (i.e.
previously unpublished) author.
| Chemical Abstracts | Econometrica | |||||
| Number of contributions | Actual | Simon's estimate | Simulation | Actual | Simon's estimate | Simulation |
| 1 | 3991 | 4050 | 4066 | 436 | 453 | 458 |
| 2 | 1059 | 1160 | 1175 | 107 | 119 | 120 |
| 3 | 493 | 522 | 526 | 61 | 51 | < td>51|
| 4 | 287 | 288 | 302 | 40 | 27 | < td>27|
| 5 | 184 | 179 | 176 | 14 | 16 | < td>17|
| 6 | 131 | 120 | 122 | 23 | 11 | < td>9|
| 7 | 113 | 86 | 93 | 6 | 7 | 7 |
| 8 | 85 | 64 | 63 | 11 | 5 | 6 |
| 9 | 64 | 49 | 50 | 1 | 4 | 4< /td> |
| 10 | 65 | 38 | 45 | 0 | 3 | 2 |
| 11 or more | 419 | 335 | 273 | 22 | 25 | 18< /td> |
 | 0.30 | 0.41 | ||||
 Science as an Evolutionary
Process
Science as an Evolutionary
Process
 The Simulation
The Simulation
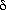 coordinate units
away from any other paper, where
coordinate units
away from any other paper, where 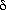 and the other
Greek symbols below are numerical parameters set at the start of the simulation). Since
distance is a well defined notion even in multi-dimensional space, the idea that kenes
and thus papers can be close does not depend on the requirement that kenes must be
located on a plane.
and the other
Greek symbols below are numerical parameters set at the start of the simulation). Since
distance is a well defined notion even in multi-dimensional space, the idea that kenes
and thus papers can be close does not depend on the requirement that kenes must be
located on a plane.
 ). Each of the
cited papers modifies the generator kene to some extent. The first such paper has the
most influence on the paper's kene, with successive citations having a decreasing
effect. A spatial way of thinking about the process is that each cited paper 'pulls' the
kene from its original location some way towards the location of the cited kene.
). Each of the
cited papers modifies the generator kene to some extent. The first such paper has the
most influence on the paper's kene, with successive citations having a decreasing
effect. A spatial way of thinking about the process is that each cited paper 'pulls' the
kene from its original location some way towards the location of the cited kene.
where m is a value between zero and one which increases randomly but monotonically for each successive citation. A similar equation determines the new y coordinate.
 ) of papers
choose a new, previously unpublished author and the rest are assigned the author of the
generator paper.
) of papers
choose a new, previously unpublished author and the rest are assigned the author of the
generator paper.
 , of each published paper acting as a generator for a further paper
at the next time step.
, of each published paper acting as a generator for a further paper
at the next time step.
 time units.
time units.
 Results
Results
| Parameter | Value |
 | 0.41 |
 | 400 |
 | 7000 |
 | 480 |
 | 0.0025 |
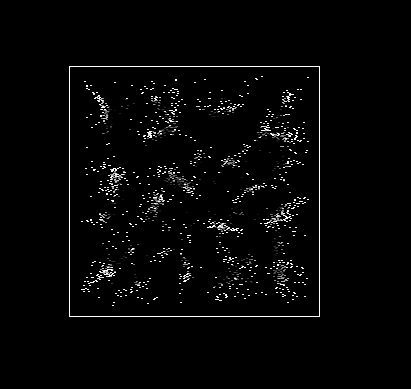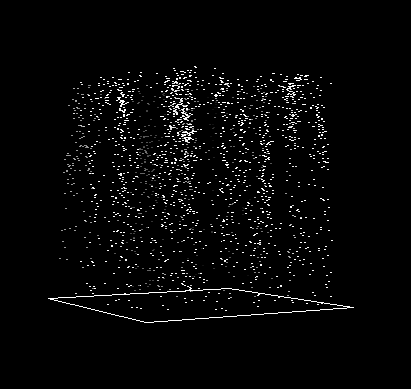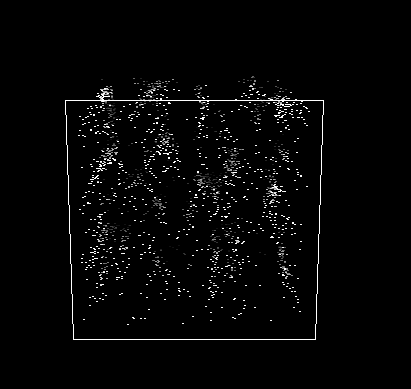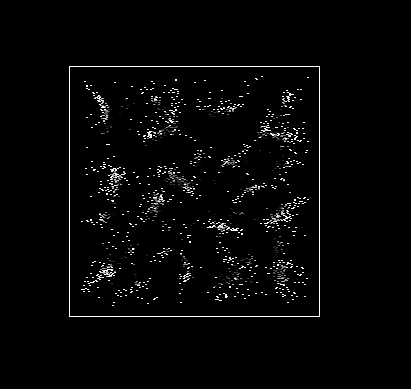
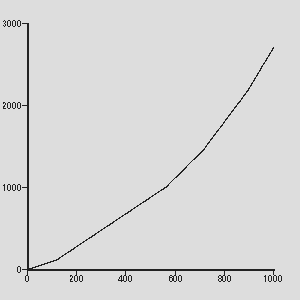
 ). The rate of growth of papers is plotted in Figure 2 and can be seen clearly in
Figure 1 where the density of dots on the plane at the end of
the simulation period is considerably greater than at the beginning.
). The rate of growth of papers is plotted in Figure 2 and can be seen clearly in
Figure 1 where the density of dots on the plane at the end of
the simulation period is considerably greater than at the beginning.
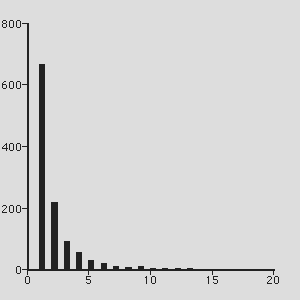
| Number of Papers | Simulation | Zipf Distribution |
| 1 | 667 | 717 |
| 2 | 218 | 193 |
| 3 | 93 | 82 |
| 4 | 56 | 43 |
| 5 | 29 | 26 |
| 6 | 20 | 17 |
| 7 | 11 | 12 |
| 8 | 9 | 9 |
| 9 | 12 | 7 |
| 10 | 3 | 5 |
| 11 or more | 15 | 24 |
(n, the number of authors, is 1,539; p, the number of papers, is 3,703;
and  is 0.41)
is 0.41)
 Discussion
Discussion
![]()
 Notes
Notes
 Acknowledgements
Acknowledgements
CONTE, R. and G. N. GILBERT (1995) 'Introduction' in G. N. Gilbert and R. Conte (editors) Artificial Societies: The Computer Simulation of Social Life. London: UCL.
CRANE, D. (1972) Invisible Colleges. Chicago: University of Chicago Press.
DAVIS, H. T. (1941) The Analysis of Economic Time Series. Principia Press.
DAVIS, L. (1991) Handbook of Genetic Algorithms. New York: Van Norstrand Reinhold.
de SOLLA PRICE, D. (1963) Little Science, Big Science. New York: Columbia University Press.
DORAN, J. and M. PALMER (1995) 'The EOS Project: Integrating Two Models of Palaeolithic Social Change' in N. Gilbert and R. Conte (editors) Artificial Societies. London: UCL Press.
DORAN, J., M. PALMER, G. N. GILBERT, et al (1994) 'The EOS Project: modelling Upper Palaeolithic social change' Simulating Societies: The Computer Simulation of Social Phenomena. London: UCL Press.
FORRESTER, J. W. (1971) World Dynamics. Cambridge, MA: Wright-Allen.
GILBERT, G.N. (forthcoming) 'The Simulation of Social Processes' in Coppock, J.T. (editor) (1997) Information Technology and Scholarly Disciplines. London: British Academy.
GILBERT, G. N. and J. DORAN, (editors) (1993) Simulating Societies: The Computer Simulation of Social Processes London: UCL Press.
GILBERT, G. N. and S. WOOLGAR (1974) 'The Quantitative Study of Science', Science Studies, vol. 4, pp. 279 - 294.
HAGSTROM, W. O. (1965) The Scientific Community. New York: Basic Books.
HANCOCK, R. and H. SUTHERLAND (1992) Microsimulation Models for Public Policy Analysis: New Frontiers. London: Suntory-Toyota International Centre for Economics and Related Disciplines.
HANNEMAN, R. (1988) Computer Aided Theory Construction. Beverly Hills: Sage.
HARDING, A. (1990) Dynamic Microsimulation Models: Problems and Prospects. Discussion Paper 48, London School of Economics Welfare State Programme.
HEGSELMANN, R. (1996) 'Cellular Automata in the Social Sciences: Perspectives, Restrictions and Artefacts' in R. Hegselmann, U. Mueller and K. G. Troitzsch (editors) Modelling and Simulation in the Social Sciences from the Philosophy of Science Point of View. Berlin: Springer- Verlag.
HUTCHINS, E. and B. HAZLEHURST (1995) 'How to Invent a Lexicon: The Development of Shared Symbols in Interaction' in G. N. Gilbert and R. Conte (editors) Artificial Societies. London: UCL Press.
JACOBSEN, C. and T. VANKI (1996) 'Violating an Occupational Sex-Stereotype: Israeli Women Earning Engineering Degrees', Sociological Research Online, vol. 1, no. 4, <http://www.socre sonline.org.uk/socresonline/1/4/3.html>.
KONTOPOULOS, K. M. (1993) The Logics of Social Structure. Cambridge: Cambridge University Press.
LATANe, B. (1996) 'Dynamic Social Impact' in R. Hegselmann, U. Mueller and K. G. Troitzsch (editors) Modelling and Simulation in the Social Sciences from the Philosophy of Science Point of View. Berlin: Springer-Verlag.
LOTKA, A. J. (1926) 'The Frequency Distribution of Scientific Productivity', Journal of the Washington Academy of Sciences, vol. 16, p. 317.
MEADOWS, D. H. (1992) Beyonds the Limits: Global Collapse or a Sustainable Future. London: Earthscan.
MEADOWS, D. H., D. L. MEADOWS, JORGE- RUUDERS, et al (1972) The Limits to Growth. London: Earth Island.
MERTON, R. K. (1968) 'The Matthew Effect in Science', Science, vol. 159(3810), pp. 56 - 63.
NOWAK, A. and B. LATANe (1993) 'Simulating the Emergence of Social Order from Individual Behaviour' in N. Gilbert and J. Doran (editors) Simulating Societies: The Computer Simulation of Social Phenomena. London: UCL Press.
O'HARE, G. and N. JENNINGS (1996) Foundations of Distributed Artificial Intelligence. London: Wiley and Sons.
PARISI, D., F. CECCONI and A. CERINI (1995) 'Kin- Directed Altruism and Attachment Behaviour in an Evolving Population of Neural Networks' in N. Gilbert and R. Conte (editors) Artificial Societies. London: UCL Press.
PATRICK, S., P. M. DORMAN and R. L. MARSH (1995) 'Simulating Correctional Disturbances: The Application of Organization Control Theory to Correctional Organizations via Computer Simulation', Simulating Societies, '95, Boca Raton, Florida.
RUMELHART, D. and G. McCLELLAND (1986) Parallel Distributed Processing, vols. I and II. Cambridge, MA: MIT Press.
SCHELLING, T. C. (1971) 'Dynamic Models of Segregation', Journal of Mathematical Sociology, vol. 1, pp. 143 - 186.
SIMON, H. A. (1957) Models of Man, Social and Rational. New York: Wiley.
WOLFRAM, S. (1986) Theory and Applications of Cellular Automata. Singapore: World Scientific.
ZIPF, G. K. (1949) Human Behaviour and the Principle of Least Effort. New York: Hafner.
 Appendix
Appendix
;;;; Simulation of Lotka's Law ;;; ;;; Based on the exposition by H.A. Simon, On a class of skew distribution functions, ;;; in Models of Man (Wiley, 1957), Chapter 9, pp. 145-164 ;;; (originally Biometrika, vol. 42, December 1955) ;;; ;;; Constants n and alpha are set to reproduce estimates for contributions to ;;; Econometrica in Table 3, column 9 of Simon (1957) ;;; ;;; Written in Common Lisp ;;; ;;; Nigel Gilbert January 14, 1996 (defparameter author-total 721) ;total number of authors (defparameter alpha 41) ;percentage probability that a paper will ; be published by a new author (defun lotka (bins) "Function to simulate the distribution of authors of scientific papers who publish different numbers of papers in a journal over some period of time. Args: BINS is a vector to hold the number of authors publishing 0 ... 11 or more papers" (let ((published (make-array n :initial-element 0)) ; element i of the array holds the ; number of papers published by ; author i (papers '()) ;list of published papers (actually consists of a list of the ; index numbers of the authors who wrote each paper) (npapers 0) ;number of papers published so far (nauthors 0) ;number of authors who have published at least one paper so far new ;index number of author of the next paper to be published bin) ;index of the vector collecting the publication distribution (do () ((= author-total nauthors)) ;go round the loop until we have ; created total-authors ;; decide who will be the author of the next new paper (cond ;; it's a new author with probability alpha ;; or it is always a new author if this is the first ever paper ((or (< (random 100) alpha) (= npapers 0)) ;; create new author (setq new nauthors) (incf nauthors)) (t ;; old author ;; select a paper at random from those already published and set the author ;; to the author of that paper (setq new (nth (random npapers) papers)))) ;; 'publish' this new paper (add it to the list of published papers) (setq papers (cons new papers)) ;; and increment the number of published papers (incf npapers) ;; note that this author has published another paper. This is the end of the loop (incf (aref published new))) ;; obtain the distribution of the numbers of authors who have published x papers ;; any who have published 11 or more are put into the top bin (dotimes (a author-total) ;for each author... (setq bin (aref published a)) ;get the number of papers this author ; has published (when (> bin 11) (setq bin 11)) ;if more than 11, set to 11 ;finally, increment the count of the ; number of authors who have published (incf (aref bins bin))))) ; this many papers (defun run (&optional (trials 10)) "run the simulated distribution TRIALS times and print out the average over the trials" (let ((bins (make-array 12 :initial-element 0))) (dotimes (i trials) ;;execute the Lotka function trials (lotka bins)) ;; times, accumulating the results ;; print out the results, after dividing each by the number of trials to get the mean (format t "Averages of ~D trials: " trials) (dotimes (b 12) (format t "~D " (round (/ (aref bins b) trials))))))
![]()
![]() Copyright Sociological Research Online, 1997
Copyright Sociological Research Online, 1997