The Modality of the Textual Institutionalisation of Literary Studies: Towards a Sociology of Literature
by Soh-young Chung
Sungkyunkwan University
Sociological Research Online, 16 (3) 3
<http://www.socresonline.org.uk/16/3/3.html>
10.5153/sro.2447
Received: 14 Oct 2010 Accepted: 15 Aug 2011 Published: 31 Aug 2011
Abstract
This paper aims to present a sociology of literary studies that is distinguished from the sociology of literature in that its focus is on literary studies as a social practice rather than as a socio-cultural institution: how literary studies is institutionalized as such not how it functions in relation to literature. The sociological analysis of literary studies in this paper entails two tasks. Firstly, it constructs a methodological frame within which literary studies can be observed and analysed in terms of the rules of discursive formation rather than as a pre-discursive entity. This is achieved through conceptualizing the Foucauldian notion of discursive formation and knowledge practice as an analytic strategy and operationalising it via Paul Dowling's Social Activity Method. Empirically, the analysis produces a description of the practice of literary studies as instantiated in the particular region of the practice constituted with what I refer to as the crisis discourse. The analysis describes literary studies as that which is emergent upon differing institutionalising strategies articulated by its participants to mark out literary studies from other practices and to maintain its disciplinarity through regulating the distribution and the access of the distribution of the discourse within and beyond the practice. The generalisability of the research in this paper lies in the applicability of the analytical method that can be employed at any given level of analysis to examine discursive practice—such as literary studies—as the effects of the particular discourses in terms of how they articulate and sustain the institutionalised identity of the practice.
Keywords: Sociology of Literature, Sociology of Literary Studies, Cultural Studies, Sociology of Knowledge, Foucault, Discursive Formation, Social Activity Method, Disciplinarity, Institutionalisation, Research Methodology
Introduction
1.1 Sociology has related to literary studies in various ways as an approach rather than a field or a disciplinary practice commonly labelled as the sociology of literature. In the most general and traditional sense, the sociology of literature refers to approaches that deal with a literary text in terms of the factors that are external to the text itself or activities that do not relate to issues of authorial creativity (Barthes 1983; Leavis 1952). It is with Marxian criticism that the sociological approach becomes a theoretically saturated enterprise in itself (Ferguson et al. 1988). The overriding thesis in the Marxian approach to literature is that literature is mirroring and so reproducing society or social reality. Although there are varying propositions across differing theories over just what is the social reality that is reflected in a literary work, the common endeavour is to connect literature and society as in concert. This line of sociology of literature, whose origin is traced back to Georg Lukács (1971) and Lucien Goldmann (1975), has developed into various theoretical tenets by British and American critics such as Raymond Williams, Terry Eagleton and Frederic Jameson. Within the discipline of literary studies it has been formulated into a species of interpretive framework such as New Historicism (Greenblatt 2005), Feminism (Gilbert and Gubar 1979), and post-colonialism (Said 1978); these—tend to be labelled as poststructuralist rather than Marxist but—nevertheless, have their ground in Marxism in one way or another. Outside the discipline of literary studies, the sociology of literature constitutes a subfield of the sociology of culture. Here literature has been examined in terms of its production and consumption as a socio-cultural institution (Bourdieu 1971; 1993); or literature is dealt with as one of the cultural media, hence attention is paid to the dynamics of the relationship between literature and the readers (see Griswold 1993; Iser 1974, 1978; Jauss 1982; Long 1985; Modleski 2008; Radway 1991, 1999). These approaches with differing disciplinary accents (See Wolff 1999) have been brought closer by cultural studies (Hoggart 1958; Williams 1961, 1977; Frow 2005).1.2 In this paper, I shall introduce a sociology of literary studies, which is distinguished from the approaches described above that can be described as a sociology of literature. The focus is on literary studies as a social practice rather than as a socio-cultural institution: how literary studies is institutionalised as such not how it functions in relation to literature. My approach here is broadly affiliated to the sociology of knowledge in the sense that it deals with literary studies, in particular the disciplinary practice in the university, in terms of knowledge practice. However, unlike the sociology of science where the empirical tangibility of the actions of producing scientific knowledge is in part captured in laboratories (see, memorably, Latour & Woolgar 1986; Knorr-Cetina 1981, 1999), the actions of literary scholars producing literary knowledge are available only in their discursive interactions occurring in textual productions. This paper, therefore, is concerned with two tasks. Empirically, it analyses a set of accounts of literary studies produced within the field of literary studies to produce a sociological description of the ways in which literary studies is conceptualised and theoretically, it seeks to address methodological issues relating to analysis of discursive practice such as literary studies.
1.3 Empirically, I define a particular group of utterances within literary studies as the object of analysis. This group of utterances is comprised of published accounts that have been recognised to constitute a particular body of debate, which is the so- called crisis of literary studies. These publications began to appear around the mid 1980s and primarily concern what literary studies is/should be in response to the growing industry of cultural studies, which was conceived as resulting in a 'paradigm shift' (Abrams 1997; Easthope 1991; Greenblatt & Gunn 1992). I call this body of utterances the 'crisis discourse' (Chung 2010). I see this crisis discourse as constituting a particular region of the practice that produces a form of self-reflexive meta-discourse defining and describing the practice in response to the 'perceived' crisis of literary studies and hence oriented toward self-validation and self-legitimation. My concern with the crisis discourse does not lie in the content of the disciplinary accounts as much as in the ways in which the accounts are validated and legitimated in relation to literary studies—claimed to be in crisis—and in relation to others' accounts. The crisis discourse, thus, is to be regarded as 'performative' in the sense that it forms a 'discursive practice that enacts or produces that which it names' (Butler 1993: 13). The crisis discourse constitutes a specific region of practice that constitutes the field of the discursive practice of literary studies in the shared feeling of crisis and it serves as the empirical setting of my research.
1.4 The principal objective of the analysis is to examine the ways in which the participants of the crisis discourse define the disciplinarity of literary studies in relation to their own discursive positions within the practice. This is to look at literary studies in terms of the ways in which it has been legitimated by its members rather than as a reified form of cultural practice such as curricular or intellectual history. However, the content of their self-descriptions and self-validations of literary studies are not the focus of the analysis. The focus is on the ways in which those self-descriptions and self-validations are produced and constitute literary studies. My interest is in looking into not what the members say and do, but how they say and do what they do as potential performatives. More specifically I look into strategies of institutionalisation, that is to say, I analyse the modality of strategies marking out the practice of literary studies from other practices and of the ways in which the discourse and the access to the discourse is distributed. Therefore, my analysis can be described as constituting a sociological description of literary studies as instantiated in the practice of the crisis discourse in the discursive moment of a putative paradigm shift.
1.5 In next two sections, I shall present the ways in which I construct the theoretical position from which literary studies is conceptualised as an object of sociological analysis, and the analytic point of view from which the crisis discourse can be observed and described in terms of its performativity. This entails discussions on Foucault's notion of discursive formation and knowledge practice especially in terms of its methodological implication and Paul Dowling's Social Activity Method (SAM) (2009), the latter discussed in detail in relation to my development of it as an analytic strategy in this paper. Then I will present an analysis of the crisis discourse in literary studies, which presents itself as an exemplar of an empirical text being interpreted as an instance of the theoretical category that is developed in the analysis, that is, as an instance of 'elaborated description' (Dowling & Brown 2010).
Construction of a theoretical gaze
2.1 To conceive literary studies in terms of its performativity is to objectify it in terms of 'discursive formation', that is to say, in terms of the ways in which it is emergent upon the plays of the rules that prescribe the object of study, subject positions, methods and strategic choices that formulate the relations of the three (Foucault 1977). The rules do not coincide with nor are they reducible to the individual text, though they might be inferred from a form of regularity in a larger group of texts. Thus literary studies, constituted as the object in this paper, cannot be 'seen' in the domain of the practice consisting of the reified forms of cultural patterns such as textual representations (Chung 2010). It refers to the level of practice where the play of the rules can be observed and this level of practice can be given higher discursive visibility when explicated in terms of Foucault's distinction between two levels of knowledge, connaissance and savoir (Foucault 1972).2.2 The distinction between connaissance and savoir is an analytic one and points to the ways in which the conceptual schema can be operationalised in relation to the object of inquiry. This is clearly explicated in the preface to The Order of Things, where Foucault explains that the archaeology is not concerned with 'descriptions of the progress of knowledge [connaissance] towards an objectivity in which today's science can finally be recognized', but to 'configurations within the space of knowledge [savoir] which have given rise to the diverse forms of empirical science [connaissance]' (Foucault 1970: xxii). Foucault explains further that the analytic focus of his 'archaeology' is the 'discursive practice/knowledge [savoir]/science axis', not the 'consciousness/knowledge [connaissance]/science axis' (1972: 183).
2.3 Discursive practices are 'embodied in technical processes, in institutions, in patterns for general behaviour, in forms for transmission and diffusion, and in pedagogical forms which, at once, impose and maintain them' (Foucault 1977: 200). The surface meaning of discursive practice is underpinned by the rules which 'govern the production, operation and regulation of discursive statements' and is mediated by power (Fox 1998: 418). 'Power/knowledge' can be construed as the analytic term for discursive practice. 'Power is not an institution, a structure, or a certain force with which certain people are endowed: it is the name given to a complex strategic relation in a given society' (Quoted in Gordon 1980: 236). Foucault's analytical objective is
[…] not that of fixing an ontologically primitive, definitively 'real' stratum of historical reality, but in tracing the mobile systems of relationships and syntheses which provide the conditions of possibility for the formation of certain order and levels of objects and of forms of knowledge of such objects. (Gordon 1980: 236)Here 'knowledge' refers to savoir. Foucault's object of investigation is the 'discursive formation' rather than set of ideas and propositions, or 'interpretative repertoires' that is available as resource for the actors to recruit prior to the interactions. The level of savoir is not what is to be discovered within the field of practice; it is what is to be constructed in analysis, in a second order description (Kennedy 1979).
2.4 'Discursive formation' refers to the regularity of the irregular distribution of statements. Regularity is a construction that is created through analysis (Anderson 2003). Analysis, therefore, is an autodidactic pedagogy and its dissemination a didactic pedagogy. The sociology of knowledge in this way is participating in the knowledge practice that constitutes the object of the sociology of knowledge, which frees it from the necessity of construction of a god's eye view. This construction of 'the point of view of the rules that come into play in the existence of such discourse [the world as such]' (Foucault 1970: xiv) is what distances Foucauldian theory from other major social theory paradigms that need to assume either the point of view of the individuals who produce utterances (the constructivist or social constructionist) or the perspective of the formal structures of the utterances (Critical theory) (Bastalich 2009).
2.5 The Foucauldian gaze is not above the social looking down over it, but rather under the social. The subliminal orientation of the gaze, however, is by no means concerned with discovering a kind of structure that is lurking under the social phenomena. Its subliminal location is an analytical level from which discourses are observed in the ways in which they are articulated. I term this gaze a 'prosthetic proprioception'. A proprioception—a term I borrow from neuroscience—may be defined as 'the reception of stimuli produced within the organism' (Merriam-Webster dictionary). It is 'the eyes of the body, the way the body sees itself' (Sacks 1970 : 47). It is the sensory feedback that enables a non-visual mapping of the body's form. The theoretical gaze I construct—consistent with Foucault's—aspires to an occupation that is analogous to proprioception in respect of the practice that it is to observe: to constitute a location, as it were, from which the 'self-movement' of the practice—that is the ways the practice becomes as such—is seen. However, this is not to be naturalised, but is the artefact of the analysis, which enables us to simulate an absent proprioception of the social and hence, it is 'prosthetic'. So it can be constructed at any level of analysis of a given practice. The theoretical gaze, distinguished from theoretical 'categories' used as forms of (meta)codification—for example, coding in grounded theory—of the observed phenomena, resists any form of totalising description of the practice or of meta-theoretical discourse. It only provides a point of view from which the social practice can be held in consistent observation and so it becomes constitutive of the practice. Social practices, from this perspective, are seen to unfold and be guided by practitioners' sense of appropriate actions, that is, strategies of action.
Operationalisation of the theoretical gaze
3.1 The prosthetic proprioception becomes an operationalisable concept drawing on more concrete materials from Dowling's Social Activity Method (SAM) (2009)[1], which is oriented towards the formulation of analytics through thorough engagement with the empirical at a level such that the distance constructed by the analytical process is not only traceable but constantly (re)interrogated. SAM's concept of the social is aligned with Foucault's concept of it as 'complex strategic relations' (Quoted in Gordon 1980: 236). It understands 'social action as consisting in autopoietic action directed at the formation, maintenance and destabilising of alliances and oppositions' (Dowling 2009).3.2 The analytical object of SAM is the structure that is emergent upon the social action. This is analogous to Foucault's discursive formation and refers to
[…] the regularity [that] is emergent upon the formation of diverse oppositions and alliances that […] carries on at all levels of analysis from state activity down to the strategies and tactics of individual players. (Dowling 2007: 174)The structure, however,
[…] is not a generative structure, but epiphenomenal and available to us only via our structural linkage with each other's material expressions, immediate (such as speech) or sedimented (such as writing). Epiphenomenal structure-as-work is thus available for us to recruit as structure-as-text into our further autopoietic social action. (Dowling 2009: 229)
3.3 SAM shares with Foucauldian theory the unique interest in the performativity of practice, not subjects or linguistic performance (Habermas 1984), to determine the form of discourse (Bastalich 2009). The methodological focus is on construction of the analytic point of view, a prosthetic proprioception in my term, which brings into discursive intelligibility the autopoietic movement of the social. The focus of analysis is not on the reconstruction of 'intersubjective meaning' as in Habermas' theory of 'communicative competence' (Habermas 1984; Lemert & Gillan 1977) but on the effects of particular discourses in respect of how they articulate 'a regime of truth' such that a particular set of rules of discourse is institutionalised. These rules of discursive formation are articulated by SAM in terms of logically complete spaces that emerge upon the relations between the individual strategies.
3.4 One of the examples of such a space is 'domains of action schema' (Dowling 1995; 1996; 1998; 2009) that was originally generated by Dowling in his sociological analysis of school mathematics textbooks (Dowling 1998). It offers a fully theorised language that enables the analysis of a given practice in terms of strength of institutionalisation in respect of the semiotic components, content and mode of expression. The institutionalisation of any practice entails the construction of a region that differentiates it from other practices; this is the esoteric domain of the practice (Dowling 1998; 2009), which is strongly institutionalised in relation to other practices in terms of both content and mode of expression. In case of mathematics, it refers to the region of the practice that deploys exclusively technical mathematical signs. The full realisation of the principles of the practice—mathematics, literary studies—is possible only within this domain. However, the subject of the esoteric domain must look beyond itself in order to ensure the sustenance of the practice by constituting a region of weakly institutionalised practice to provide 'pedagogic portals' (Dowling 2009), where the discourse of esoteric domain is recontextualised in terms of everyday practice and the access to the esoteric domain is simulated. This is referred to as the public domain, which is the product of the 'recontextualising gaze' of the esoteric domain. It is weakly institutionalised in relation to other practices in terms of both content and mode of expression. This would be the region of practice that is concerned with applications of mathematics where mathematical formulas are expressed in terms of shopping activities, for instance. The combination of differing strength of institutionalisation of content and mode of expression respectively generates two more domains: the descriptive and the expressive. The descriptive domain refers to those regions in the practice that institutionalise content weakly in relation to other practice, but institutionalise expression strongly. This may be illustrated in terms of mathematical modelling where mathematical symbols are used to signify non-mathematical objects and relations. The expressive domain refers to those regions that institutionalise content strongly, but institutionalise expression weakly, in which a non-mathematical signifier may be recruited to refer to a mathematical object—an equation is a balance, for instance. These four domains are shown in the schema in Figure 1.

|
| Figure 1. Domains of Action (Dowling 2009) |
3.5 The esoteric/public domain distinction resonates with Fleck's 'esoteric circle' and 'exoteric circle'. An esoteric circle is composed of 'specialist' members who are engaged with the rules and principles of the 'thought collective', while an exoteric circle is composed of members who adhere to the rules and principles produced by the members of the esoteric circle but have no direct access to the realization of the rules and principles themselves (Fleck 1979; [1936]1986). However, whilst Fleck's terms refer to the state of a 'community' of practice, Dowling's terms are initially limited to strategies that are available within the practice. The state of the practice (of the community of practice) emerges from the deployment of these strategies in the texts of the practices, which is to say, in the utterances and actions of members of the community. The schema thus neither represents a set of categories into which types of discourse are filed nor a structure of the event of discourse, but a space within which what is said becomes discursively intelligible in its being constitutive of the practice. The schema constitutes a prosthetic proprioception within the practice, a point of view from which a practice can be described in terms of its self-movement.
3.6 SAM exhibits some superficial resemblance with Actor Network Theory (ANT), which is proposed as 'techniques of power/knowledge' (Law 1986) or as 'scaled-down versions of Foucault's discourses' (Law 2007) focusing on the relational performativity of actors/actants rather than the individual entities. Law's expression of affinity between ANT and Foucault's theory is, however, confined to the most general level of the view of the social that it operates upon precarious and strategic relations. The relations that are examined by ANT are delimited to those that extend links through enrolling allies. ANT is oriented on the ways in which one privileged network of the 'heterogeneous' alliances formed between 'actants' is built over the myriads of possibilities, a narrative of success (Couldry 2008). An actor network is offered as a form of stabilised entity which enacts 'power' and control. Once it is constructed, the actors become functionaries whose language and actions are determined by the network. Focusing on the construction of actor networks, thus ANT is deficient in terms of the analysis of the process of institutionalisation, that is, why it is that some practices become institutionalised while others do not. It also stops short of investigating how actors understand and interpret the network of which they are constituent. This excludes the opportunity to examine the instability of power relations and hence ignores the space for resistance and opposition. This constitutes a key difference from SAM whose analytic scope includes the conditions of possibility of destabilisation. SAM offers a constructive description of a practice in terms of relational space that makes intelligible the ways in which the practice emerges upon ongoing social action of the formation, maintenance and destabilising of alliances and oppositions.
3.7 Another important aspect of ANT that is distinct from SAM is its reliance on the ontological limit of actants. Actants are, according to Latour, the things 'behind the scientific texts' (1987: 89). An actant is defined by the part it plays in the network in relation to others, that is, by its performance in the particular network. However, it is not ontologically empty; it is 'something' and 'this something is progressively shaped by its re-actions' to the conditions imposed on it (Latour 1987: 89). The performance, thus, presupposes a 'competence' (Ibid.) that is inherent in that 'something'. ANT focuses on unfolding the process of the 'essence' of things 'slowly unveiled through each of […] its manifestations (Ibid.) rather than explains 'the condition' that configures the performance of the actants in certain ways. Actants are conceived in socially purified forms: 'things-in-themselves'. ANT shows that what we see is the result of the ways in which actants are connected in certain ways by which the actants are made to play different roles. An actor-network, however, 'refer[ring] to the provisional assembly of productive, heterogeneous and [...] quite limited forms of ordering located in no larger overall order (Law 2007)', 'does not explain, or even address, agents' interpretations of those networks and their resulting possibilities of action' and hence does 'not offer a way of analyzing social action' (Couldry 2008).
3.8 This inevitably etic gaze further distinguishes ANT from SAM whose gaze—prosthetic proprioception—is constructed within the practice. SAM constructs a level of analysis that addresses the ways in which actors understand and interpret the relations and articulate their interpretation. The actors' actions are already sociological in this sense: they are based on the actors' observation of the social in the form that is reified as an objective structure. The sociology of knowledge then is inevitably a second-order observation and in this way the analytic point of view can be constructed without having to construct a reference point either in the originating consciousness or outside of the practice. The social 'reality' is always viewed through the actors' strategic actions without losing its full contingency. This particular analytic strategy of SAM enables both analysis of the strategic relations in a micro-level of practice and systematic description of the ways in which the relations are made possible. SAM in this respect then also complements Goffman's micro-interactionist approach that does not offer much in terms of understanding how the interactions are linked to larger social structures or how institutions come into being as such (Chriss 1995; Hacking 2004). In both Goffman's approach and SAM, interpersonal interactions (in the case of SAM, interactions at any level of analysis) are conceived as the core unit of the social. However, whilst in Goffman's actions are viewed as 'performances' (Goffman 1959), in SAM they are viewed as 'performatives'. In Goffman's, the analysis tends to be based on the intentionality of the performer that is ultimately empirically unavailable and hence it concerns individual strategies predicated upon given contextual contingencies, whereas SAM is interested in examining strategies that are available within a practice and works at a more constitutive level, forming the contextual contingencies themselves.
3.9 SAM's value lies in its being method through which the theoretical and methodological constructions can be operationalised in an encounter with the empirical enabling analysis of the strategic relations at any given level of analysis. It offers the proprioception in a form of analytics, which Dowling refers to as an 'organisational language' (Dowling 2009), part of which I am deploying in my analysis of literary studies in this paper.
Method: Reconstruction of the domains of action schema
4.1 I shall deploy the 'domains of action schema' explained in the previous section in order to analyse literary studies. My use of the schema in this paper is developmental in two ways. I shift, firstly, to another empirical setting—a different discipline. This introduces an issue that relates to the peculiar nature of the textual practice of literary studies. It is rather difficult to distinguish the expressive/descriptive domain in this area because there is extensive continuity between the literary and the non-literary languages at the semiotic level, which is to say, literary studies lacks strongly institutionalised expressions such as algebraic and logic symbols used in mathematics. It is comparatively difficult to find an aspect of the practice that could be described as constituting the expressive/descriptive that might be equivalent to the examples given by Dowling concerning mathematics textbooks (see Dowling 1998; 2009)[2]. Therefore, I reconstruct the schema only with the esoteric/public domain here and this can be generalised in relation to practices that have not reached a high level of discursive formation.[3]4.2 Secondly, I deal with a practice at the level where self-reflexive practice occurs. In this paper I especially focus on works of authors whose discourses are produced from positions that are concomitant with their respective practices of literary criticism. My analysis of the crisis discourse is concerned with how institutionalising strategies within literary studies bear upon one another, the strategies entailing conceptualising the disciplinarity of literary studies that entails the act of producing critical commentary on literary texts. The analysis is rendered, in this way, to its maximum power encompassing the highest level of complexity of the given level of practice. This requires the construction of an analytic strategy that enables 'shaping a specific gaze that allows the environment to appear as consisting of the observations of other people or systems [the crisis discourse]' (Andersen 2003: vi) that consist of the observations of systems (literary criticism). I articulate the extra level of analysis through complicating the schema with extra layers of domains in the mis-en-abyme fashion. I extend and change the layout of the schema presented in Figure 1 to express this complication and this new form is presented in Figure 2.
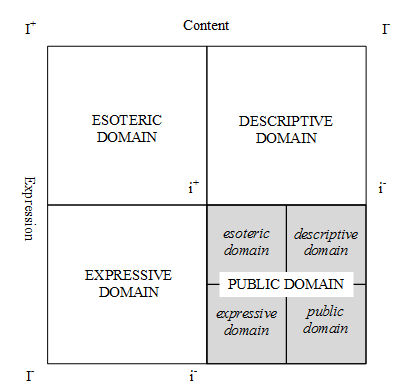
|
| Figure 2. Domains of Action in Meta-discourse Practice[4] |
4.3 The greyed bottom right quadrant represents literary studies at the level at which it is identified as the practice of literary criticism. It can be described as being constituted with the esoteric domain where 'literary discourse' is generated—for example, critical interpretation of Shakespearean sonnets—and the public domain where the literary discourse is recontextualised in lay languages—for example, Shakespearean sonnets are introduced in the context of emphasizing the importance of love in ordinary lives. The crisis discourse then constructs a gaze that enables a meta-description of the practice of literary criticism in terms of the ways in which the esoteric domain is/should be maintained in relation to the public domain. This constructs another level of esoteric practice that constructs the whole domain of literary criticism as the public domain via which the newly generated disciplinary discourse is distributed. My use of the term mis-en-abyme not only refers to the graphic result of expressing this two level practice where an image (a domain of practice) contains a copy of itself (another domain of practice), but also to the self-reflexivity in the reproduction of the domain.
4.4 In the following sections I shall present my analysis of the crisis discourse. The analysis originally dealt with nine book-length publications[5] and it yielded three modes of strategies of institutionalising literary studies. In this current paper, I will present the analysis of three each representative of the three modes of institutionalising strategies respectively. I will start my analysis with a consideration of a work by Stanley Fish (1995) whose institutionalising strategy constitutes a radical exception in the respect that it requires only a single domain.
Institutionalising literary studies by purifying the gaze
5.1 Fish's (1995) concept of the disciplinary practice of literary studies is grounded in a strong conventionism. In his conceptualisation, literary studies operates like Kuhn's scientific community (Kuhn 1970) in that objects of study ('puzzles') and choice of interpretive schemes ('solution') are defined by the practice itself. The esoteric domain of the practice is constituted with the literary conventions and operates as a closed self-generating practice. One's interest in particular texts, methods, and even innovative attempts to read the texts are always already configured by the professional practice he/she is engaged in. Fish explains:[…] there will be a new understanding of the profession's decorums, but those decorums will still be specific to the profession's practice, which will be internally altered, but not necessarily altered in its relationship to other practices, like the practice of politics, from which it will continue to be distinguished. (Fish 1995: 44)In this context, a text that is recontextualised by the gaze constructed from the esoteric domain is absorbed into the esoteric domain: 'literary interpretation […] has no purpose external to the arena of its practice' (Fish 1995: 113). Construction of the public domain is not a possibility in this conceptualisation.
5.2 Therefore, in Fish's view, any interpretive framework, no matter how politically impregnated, cannot be other than literary theory; a 'political' reading, however subversive it is claimed to be, is simply an alternative mode of reading as long as it has been engendered within literary studies, 'within the professional context of his labours' (Fish 1995: 48). The political aspiration of New Historicism and cultural materialism is never viable other than as a form of literary interpretative scheme, according to Fish. Fish's objection to New Historicist and cultural materialist approaches is, then, concerned with not so much the textual nature of their critical commentaries as their prurient gaze towards the political discourse cast beyond the esoteric domain. This prurient gaze is discursively articulable as the construction of a public domain—the domain rejected by Fish—by using the language of the domains of action schema.
5.3 The political discourse of the New Historicist and cultural materialist reading constructs a space where literary criticism is brought into alignment with the non-literary discourse and hence via which the access to and the distribution of literary discourse is offered outside the esoteric domain. Fish argues, for example, that Raymond Williams' reading of pastoral is
not merely urging scholars to approach literary materials from a new angle; he is asking them to confront the implication of the practice in ways that do not allow them to think of it as 'merely literary'. (Fish 1995: 46)
5.4 The contextual information such as social and historical factors relating to a literary text is brought in to enhance not only the understanding of the 'semantic density' (Fish 1995: 13) of the text but also a historical understanding of a particular society or a view of "a social order" (Williams 1975: 46). This kind of reading constructs a gaze that invites the reader to look outward from literary studies rather than learn to be in it. A literary text is not only recontextualised as the object of the literary gaze but serves as a reference to socio-historical facts. The political discourses of New Historicism and cultural materialism constitute the rationale of the construction of the public domain, by which the access to and the distribution of literary discourse is offered outside the esoteric domain of literary studies itself. The gaze in Fish's practice is self-referential while the gaze in the New Historicist and cultural materialist practice refers to non-literary practices.
5.5 Fish's construction of opposition to the non self-referential gaze in relation to New Historicism and cultural materialism can be described as a strategic move to purify the gaze. The gaze Fish is constructing is close to Bourdieu's (1993) 'pure gaze'—a product of the practice of literary studies referring to nothing but itself. Fish pronounces that "[l]iterary interpretation, like virtue, is its own reward" (1995: 110). Purifying the gaze entails regulating access to the esoteric discourse other than via apprenticing to the discourse. The entire practice of literary criticism is confined to the esoteric domain within which no region is allowed to open up to liaise with other practices. The dynamism of the esoteric domain practice is internally generated and contained within the practice.
Institutionalising literary studies by purifying the object
6.1 In contrast with Fish, Eugene Goodheart (1999) conceives literature as external to the practice of literary criticism. The meaning of literature is not constructed by literary criticism; it is inherent in the literary text. Literary criticism and literary texts constitute two distinct realms of practice. The esoteric domain practice of literary studies is constituted with the particular mode of transaction with a text, which recognises and articulates the domain of the meaning of a literary text that is not accessible by other modes. This particular mode of transaction is described as the practice of 'literary sensibility' (Goodheart 1999). Literary sensibility enables the recognition of the 'wholeness and autonomy' (Goodheart 1999: 74) of a literary text, hence judges what is 'literature' and what is not. For example, here is how Goodheart argues for the difference between the significances of the bloody scenes in The Iliad and in a TV show:[…] a classic may resist the interests and fashions of the age, even offend against them, and yet persist in being lively to us because of the imagination, intelligence, and force of the resistance. What is more foreign to our pacifism than Homer's celebration of Achilles' wrath or to our humanism that Swift's or Nietzsche's misanthropy? This resistance forces us to examine what we have perhaps repressed in ourselves-our own bloody-mindedness that revels in spectacles of mayhem or our distaste for most human encounters. (We encounter bloody-mindedness and bloody acts daily on the TV screen, but in a form that doesn't challenge us to reflect upon our capacity for mayhem. The Iliad does.) (Goodheart 1999: 50)The difference between The Iliad and a TV show is articulated in terms of what they do to us. A highly localised experience of reading is given in support of Goodheart's claims about the value of The Iliad that surpasses that of TV shows and transcends socio-historical contexts.
6.2 The description and interpretation of The Iliad is epistemologically prior to the articulation of the literary sensibility that judges the value of The Iliad. Literary sensibility is theoretically inarticulate. It is only demonstrated through the description and interpretation of a literary text: hence, the literary text that is chosen as the object of criticism constitutes the evidence of literary sensibility a posteriori. Goodheart goes on to say that 'we cannot know whether Homer has value unless he has been experienced' and the failure to recognise its value would lie with the reader's inadequacy (Goodheart 1999:57). However, the evaluation of the quality of the reader's response must be grounded in the already existing responses that are established as 'legitimate' ones. Their legitimacy is grounded in the selection of the right text since the literary text is the instance of literary sensibility. Literature or the authors of literature is/are, therefore, circularly presented as the origin of the gaze of the esoteric domain and the principles of reading.
6.3 In Goodheart's discourse, the disciplinarity of literary studies is conceptualised in terms of literary sensibility. The texts that are recontextualised by the esoteric domain gaze (literary sensibility)—those that can be called 'literature'—constitute the strongly institutionalised region in the public domain: in other words, literary sensibility is recontextualised as literature which is in a form that is transmissible to and accessible by non-literary readers. This can be shown using the domains of action schema as in Figure 3:
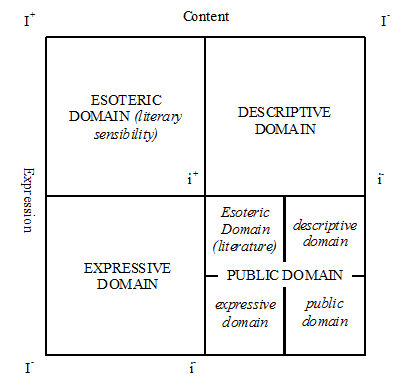
|
| Figure 3. Domain of Action in the Crisis Discourse 1 |
6.4 The public domain is strongly institutionalised at the level of the object. Literature becomes the reification of the esoteric domain gaze, i.e. literary sensibility, and it brings non-literary practices into alignment with literary sensibility. The strongly institutionalised region in the public domain comprising literature is like an art gallery where selected art works are exhibited and offered to the public. Anyone who walks in the gallery and appreciates the works exhibited there is endowed with quasi-membership of the art practice. Anyone who participates in reading and appreciating 'literature' that are institutionalised as such is endowed with quasi-membership of the practice of literary sensibility.
6.5 The strength of institutionalisation of literary studies is constructed by purifying the object. The strategy of purifying the object appears in the form of externalising a literary text as an object of passion to some extent rather than that of critical investigation. This becomes apparent when literary sensibility is associated with 'love' of a literary work, which is described as 'empathy with creative achievement' (Goodheart 1999: 79). The foremost quality for literary critics is 'enthusiam' or 'love' for their subject (Goodheart 1999) and their mission is to transmit that love by mediating literature to students. The role of a critic is that of a priest, a transparent mediator of the meaning, whose profession is to be defined by the devoutness and passion for the sacred words of literary work. Literary studies is not so much about formulating theories to discriminate literature from other texts as about preserving and transmitting and celebrating it. Thus, the primary reason for the objection to theoretical criticism—feminism, post-colonialism and deconstruction are the specific examples provided by Goodheart—is its deference of the meaning of a literary text to a theory: a literary text is recruited as an instance of tenets of a theory. This constitutes 'systematic resistance to texts' displaying a 'deconstructive animus against humanistic assumptions of the wholeness and autonomy of works of literature' (Goodheart 1999: 74).
6.6 Literary studies conceptualised by Goodheart can be described as an institutional practice of the love of literature. The alliance between members of the practice centres on literature, and this shows affinities with that of a fan community in that literary work is constructed as the sole source of rules and principles of the practice. Literary criticism is a passionate act of consuming literary work and the relation of the literary critic to literature coincides with that of the fan. The literary critic might be called an 'aca-fan' (Hills 2002; Jenkins 1992).[6] From this point of view, the antagonism between different practices such as Fish's and New Historicism or cultural materialism are then not so much between competing teams in the same field as between fans of different objects.
Institutionalising literary studies as cultural studies
7.1 Another distinct line of discourse within the crisis discourse is concerned with conceptualising literary studies as cultural studies in which literary texts are conceived of as means of achieving critical literacy.7.2 Patrick Brantlinger (2001) suggests that traditional literary studies has been structured around utopianism. The aesthetic dimension that has been emphasised in literary studies is associated with utopianism either in terms of "Arnoldian humanism, with its stress on the supposed power of literature to humanize the individual into her [sic] 'best self'", or in terms of "the promesse de Bonheur inherent in the experience of the beautiful" (2001: 35). Brantlinger argues that this traditional way of framing literature as a provider of an aesthetic experience that serves as an alternative vision of harmony to the sordid reality has been operating as a form of authority in linking texts to contexts in a particular way. He proposes to (re)conceptualise literary studies as a discourse that enables a critique of unequal distribution of access to the aesthetic. The esoteric domain that is constructed in this kind of conceptualisation is constituted with the discourse of theories that recontextualises literary studies in terms of a "heterotopian" vision[7]:
[…] the burgeoning of often conflicting literary and cultural theories, no one of which serves as a unifying orthodoxy as the New Criticism perhaps did for a while, is clearly heterotopian, especially given that many of the theories stress differences, performativity, and the postmodern fragmentation and pluralisation of experience both real and imagined. (Brantlinger 2001: 46)Here literary texts are established as means to achieve 'critical literacy' giving rise to an understanding of socio-economic inequality and cultural monopoly and ultimately the emancipation of the oppressed. The esoteric domain is constituted with the discourse of Marxism and poststructuralism, and pedagogic theories that enable the construction of a curriculum that is 'inclusive, democratic, and multicultural rather than exclusive, authoritarian, and monocultural' (Brantlinger 2001: 124). Literary texts constitute the curriculum along with emancipatory theories.
I take it as hopeful that much that had been excluded from academic canons and contexts is now being included. In various ways, postcolonial, cultural and race and ethnic studies are mutually reinforcing, and can be expected to gain strength in higher education. Together with feminism and "queer theory", the political goals of all of these studies are democratic and broadly emancipatory. (Brantlinger 2001: 12)
7.3 The curriculum as an emancipatory form plays an important role in giving students an active and critical voice, the ability to express themselves on the basis of their own mundane experience. The curriculum constitutes the strongly institutionalised region in the public domain practice.
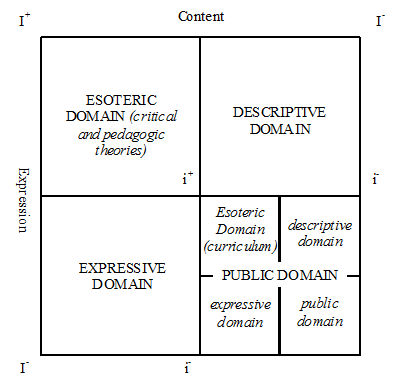
|
| Figure 4. Domains of Action in the Crisis Discourse 3 |
7.4 The curriculum is offered as an instance of the esoteric discourse, a reified form of the emancipatory theories that is transmitted to and recruited by individuals to deal with their own social situation. The pedagogic aim for literary studies is not to apprentice students into the literary discourse but to help students "be better prepared for the future" (Ibid.: 149). The rationale for the construction of the public domain consists in "ethical and political imperatives" (Ibid.: 124). Brantlinger maintains:
[I]t is possible to construct, with the aid of one or more emancipatory theories, images of collective experience free of domination. It is the task of emancipatory theory to enable the construction of such images and to encourage the hope that they can be realized in practices both locally and globally, both among individuals and among all cultures and societies. (Brantlinger 2001: 67)
7.5 Brantlinger's strategy to institutionalise literary studies constitutes an opposition to Fish's move by making the construction of the public domain an essential part of the practice of literary studies. Brantlinger denies the productivity of the practice of recontextualisation, of turning the esoteric gaze outward inflating it with 'impure', non-literary desire. On the other hand, he contradicts Goodheart's strategy of purifying the object by removing literary texts from their privileged status. Literature is replaced with a curriculum as the institutionalised region in the public domain through which the esoteric discourse of literary studies is distributed.
Idealisation of literary knowledge
8.1 In the preceding sections, I have analysed the metadiscourses of the three authors in respect of theie strategies of institutionalising literary studies. From this analysis, a description of the differing strategic moves at another level is arising: proselytising literary knowledge. The differing strategies to institutionalise literary studies can be mapped out at the level where the meta-discourse strategy of the crisis discourse is regarded as an act of 'marketing'. This is about attempting to legitimise the practice through establishing public accountability, seeking alliances beyond the practice. This is concerned with the ways in which the authors engage in both esoteric domain and public domain strategies in relation to proselytising their practice. I call these 'strategies of idealising disciplinary (literary) knowledge'. Literary practice is idealised to the extent that it has values that transcend the disciplinary limit. Combining the public domain and esoteric domain according to relative emphasis given to them gives rise to a relational space as in the schema in Figure 5.

|
| Figure 5. Modes of Idealising (Literary) Disciplinary Knowledge |
8.2 Fish recruits a strong esoteric domain strategy and a very weak public domain strategy. I have shown in the preceding analyses that Fish institutionalises literary studies by purifying the gaze. He conceptualises literary studies as a self-referential system, hence constructing no public domain or, perhaps, a public domain as no more than a doorway. The institutionalisation of literary studies operates via the regulation of the distribution of the discourse beyond the esoteric domain and of access to the discourse other than by participating in the discourse. In this formulation, the practice of literary studies forms a kind of 'private' club. The practice operates in a coherence that refers to self-referentiality and closure. It is legitimated by the virtue of its own existence. Fish's strategy can be described as occulting the practice of literary studies.
8.3 In contrast with Fish, Goodheart constructs a public domain of literary criticism within which literature is constructed as a comparatively strongly institutionalised region proffered as a quasi access to the esoteric discourse. The institutionalised practice of literary studies is to be primarily operated through the purification of the object, literature, through which literary discourse is reified and distributed beyond the esoteric domain. So It can be claimed that Goodheart recruits a very strong esoteric domain strategy having literary studies cast its esoteric gaze onto non-literary practice via literature, which is a reified form of the esoteric gaze. He also employs a relatively strong public domain strategy in that offering literature as a reified form of the esoteric gaze through which the literary discourse is brought into alignment with other discourses. I describe this as an evangelising strategy. The esoteric practice of literary studies is distributed in the form of programme (which is reified as the canon) that refers to other practices in the way that privileges the esoteric gaze. This is a move that brings practices beyond the literary into alignment with literary studies by proselytising literary studies as offering a whole way of life.
8.4 The strategy demonstrated by Brantlinger involves the construction of the public domain and the recontextualisation of literary discourse as that of literacy offered in the form of an emancipatory or enlightening curriculum. The curriculum constitutes an institutionalised region in the public domain through which the emancipatory theories of the esoteric discourse are brought into alignment with the student's own social condition. This strategy maximises the public domain practice offering the curriculum as a medium through which access to discourses other than the literary is achieved. This is a strategy of reification. The maximising of the public domain practice moves to totalise practices beyond the literary by cutting loose the esoteric domain to have the reified gaze of the practice operate as a transcendent discourse. Some observations made on the hegemonic move made by literary studies turned cultural studies are relevant. This new form of literary studies is seen to have become a 'discourse' and a programme that defines other activities in the humanities (Simpson 1995), or to have been overtaking other disciplinary areas (Appadurai 1996).
8.5 The bottom right space defined by weak public domain strategy and weak esoteric domain strategy constitutes the exact obverse of Fish's strategy, which can be described as strategy of counter-institutionalising. Richard Schwartz's (1997) discourse exhibits this strategy. His conceptualisation of literary studies constructs no institutionalised esoteric domain. Literary criticism is operated on the level of the individual, which is why I excluded his book from the analysis in this paper that focuses, rather, on explicating institutionalising strategies. The gaze that is cast onto literary texts advocated by Schwartz is purely contingent upon the 'gazer', which could be a synthesis of any discourses that are available. Literature or literary studies in any form of institutionalised practice is rejected.
Conclusion
9.1 I set two objectives at the beginning of this paper. One was the production of a sociological description of the practice of literary studies as instantiated in what I have referred to as the crisis discourse. The other was to establish a methodological frame within which discursive practice such as literary studies can be established as an empirical object amenable to such sociological analysis. I have achieved the latter through firstly adopting the Foucauldian notion of discursive formation and knowledge practice, in particular articulating the analytic distinction between connaissance and savoir, as a theoretical gaze. Discursive formation concerns the level of savoir where a practice can be described in terms of the process of its configurations rather than as a set of ideas or propositions—the level of connaissance. I have conceptualised this particular theoretical gaze as the prosthetic proprioception, an analytic point of view whereby an internal perception feels the movements of the practice as its own limbs. Finally, I have operationalised it via SAM. My deployment of SAM's domains of action schema, in particular, has enabled an examination and description of literary studies as instantiated in the crisis discourse as that which is emergent upon these complex relations configured by various lines of alliances and oppositions among different discourses.9.2 In the analysis presented in this paper, I have constructed two kinds of prosthetic proprioception. One is the extended domains of action schema and the other is the modes of idealising disciplinary knowledge. The former has enabled me to observe and describe in a consistent language differing strategies of institutionalising literary studies marking its esoteric practice and regulating the ways in which it is distributed and accessed. The latter enabled me to describe these varied strategies at another level where I can bring them together and organise them in another relational space. These two level analyses provide a picture of how literary studies is institutionalised in terms of both its inimitable distinctiveness and its public accountability in relation to other practices.
9.3 The analysis of the crisis discourse in literary studies, moreover, shows a way of seeing the disciplinarity of literary studies as the effects of particular discourses in terms of how they articulate and sustain the disciplinary identity of literary studies as such rather than as a pre-discursive entity. The generalisability of my research is, however, 'theoretical' (Dowling & Brown 2010: 151) and lies not so much in the generalisability of the description of literary studies as a knowledge practice in relation to other practices as in the applicability of the theoretical gaze and the analytical method that can be employed and deployed as an approach to the analysis of a wide range of discursive practices.
Notes
1See http://pauldowling.me/SAM for further theoretical exposition of SAM and a range of existing analytics developed out of various empirical contexts.2Although, of course, literary studies varies in this respect. New Criticism would institutionalise a set of specialist terminology, thus rendering a descriptive domain possible, as would Theory. Categories from these areas might also be rendered using non-specialist terms (expressive domain). The distinction with respect to mathematics is that the latter presents its institutionalised expression in what is generally a more strongly delineated way; literary studies will wrap its terminology in less strongly institutionalised language (in terms of expression) and this terminology is often also incorporated into the discourse of other practices, for example, terms such as 'paradox', 'ambiguity', 'irony', etc. In respect of the latter point, we might say that much of literary discourse is expressive domain.
3Foucault distinguishes four types of threshold to describe the emergence of discursive formation: positivity, epistemologization, scientificity and formalization. Foucault describes mathematics as the only discursive practice to have crossed at once and the same time the four thresholds (1972: 188).
4The same form has emerged and been employed in Jeremy Burke's analysis of the construction of the school mathematics curricula (working paper) (see Dowling 2009, c.12).
5Bergonzi (1990); Berube (1998); Brantlinger (2001); Ellis (1997); Fish (1995); Goodheart (1999); Hilfer (2003); Kernan (1990); Scholes (1998)
6Hills (2002) distinguishes between 'aca-fan' and 'fan scholar' according to the primacy of the identity: the former indicates the academic as its primary identity and the latter is identified primarily as a fan. Jenkins's use of 'fan critic' (1992) is consistent with 'fan scholar'. The members of The Republic of Pemberly, a community composed of fans of Jane Austen, for example, are fan critics. (see Chung, Dowling & Whiteman 2004)
7The specific discourse on which Brantlinger's concept of 'heterotopia' is based is Foucault's theory (1986).
References
ABRAMS, M. H. (1997) The Transformation of English studies: 1930-1995. In T. Bender & C. E. Schorske (Eds.), American Academic Culture in Transformation. Princeton, New Jersey: Princeton University Press.
ANDERSON, N. A. (2003) Discursive Analytical Strategies: Understanding Foucault, Koselleck, Laclau, Luhmann. Bristol, UK: The Policy Press.
APPADURAI, A. (1996) Diversity and Disciplinarity as Cultural Artifacts. In C. Nelson & D. P. Gonkar (Eds.), Disciplinarity and Dissent in Cultural Studies. New York; London: Routledge.
BARTHES, R. (1983) On Racine (R. Howard, Trans.). New York: Performing Arts Journal Publications.
BASTALICH, W. (2009) Reading Foucault: Genealogy and Social Science Research Methodology and Ethics. Sociological Research Online, Vol.14, no. 2. <http://www.socresonline.org.uk/14/2/3/html>, last accessed 1/10/2010.
BERGONZI, B. (1990) Exploding English. Oxford: Clarendon.
BÉRUBÉ, M. (1998) The Employment of English: Theory, Job, and the Future of Literary Studies. New York; London: New York University Press.
BOURDIEU, P. (1971) Intellectual Field and Creative Project. In M. F. D. Young (Ed.), Knowledge and Control (pp. 161-188). London: Collier-Macmillan.
BOURDIEU, P. (1993) The Field of Cultural Production: Essays on Art and Literature.Cambridge: Polity.
BRANTLINGER, P. (2001) Who Killed Shakespeare? New York; London: Routledge.
BROWN, A., & DOWLING, P. (1998) Doing Research/ Reading Research: A mode of interrogation for education. London: Falmer Press.
BUTLER, J. (1993) Bodies that Matter. New York: Routledge
CHRISS, J. J. (1995). Habermas, Goffman, and Communicative Action: Implications for Professional Practice. American Sociological Review, 60, 545-565. [doi:://dx.doi.org/10.2307/2096294]
CHUNG, S.-y., DOWLING, P. C., & WHITEMAN, N. (2004) (Dis)possessing Literacy and Literature: Gourmandising in Gibsonbarlowville. In A. J. Brown & N. Davis (Eds.), The World Yearbook of Education 2004: Digital Technology, Communities and Education (pp. 74-94). London: Routledge.
CHUNG, S.-y. (2009) The Crafting of Crisis: A Sociological Analysis of the "Cultural Studies Paradigm Shift" in Literary Studies. Unpublished Ph.D Thesis, Institute of Education, University of London, London.
CHUNG, S.-y. (2010) Talk about a Crisis!: A Sociological Analysis of the 'Crisis Discourse' in Literary Studies. The International Journal of the Humanities, vol. 8, no. 3 pp. 175-186.
COULDRY, N. (2008) Actor Network Theory and Media: Do They Connect and on What Terms? In A. Hepp, F. Krotz, S. Moores & C. Winter (Eds.), Connectivity, Networks and Flows: Conceptualizing Contemporary (pp. 93-110). London: Hampton Press.
DOWLING, P. (1995) Discipline and Mathematise: the myth of relevance in education. Perspectives in Education, vol. 16, no. 2 pp. 209-226.
DOWLING, P. (1996) A Sociological Analysis of School Mathematics Texts. Educational Studies in Mathematics, vol. 31 pp. 289-415. [doi:://dx.doi.org/10.1007/BF00369156]
DOWLING, P. (1998) The Sociology of Mathematics Education: Mathematical Myth/ Pedagogic Texts.London; Washington D.C.: Falmer Press.
DOWLING, P. (2007) Quixote's Science: Public Heresy/Private Apostasy. In B. Atweh et al. (Ed.), Internationalisation and Globalisation in Mathematics and Science Education (pp. 173-198). Dordrecht: Springer. [doi:://dx.doi.org/10.1007/978-1-4020-5908-7_10]
DOWLING, P. (2009) Sociology as Method: Departures from the Forensics of Culture, Text and Knowledge. Rotterdam: Sense.
DOWLING, P. & BROWN, A. (2010) Doing Research/Reading Research: Re-interrogating Education (2nd ed.). London: Routledge.
EASTHOPE, A. (1991) Literary into Cultural Studies. London; New York: Routledge.
ELLIS, J. M. (1997) Literature Lost: Social Agendas and the Corruption of the Humanities. New Haven: Yale University Press.
FERGUSON, P. P., DESAN, P., & GRISWOLD, W. (1988) Editors' Introduction: Mirrors, Frames, and Demons: Reflections on the Sociology of Literature. Critical Inquiry, vol. 14, no. 3 pp. 421-430. [doi:://dx.doi.org/10.1086/448448]
FISH, S. (1995) Professional Correctness: Literary Studies and Political Change. Cambridge, Massachusetts; London, England: Harvard University Press.
FLECK, L. (1979) Genesis and Development of a Scientific Fact (F. Bradley & T. J. Trenn, Trans.). Chicago and London: The University of Chicago Press.
FLECK, L. ([1936] 1986) The Problem of Epistemology. In R. S. Cohen & T. Schnelle (Eds.), Cognition and Fact (pp. 79-112). Dordrecht; Boston; Lancaster; Tokyo: D. Reidel Publishing Company.
FOUCAULT, M. (1970) The Order of Things: An Archaeology of Human Science. London: Tavistock.
FOUCAULT, M. (1972) The Archaeology of Knowledge and the Discourse on Language (A. M. S. Smith, Trans.). New York: Pantheon Books.
FOUCAULT, M. (1977) History of Systems of Thought. In D. F. Bouchard (Ed.), Language, Counter-memory. Practice (pp. 199-204). Ithaca, New York: Cornell University Press.
FOX, N. J. (1998) Foucault, Foucauldians and Sociology. The British Journal of Sociology, vol. 49, no. 3 pp. 415-433. [doi:://dx.doi.org/10.2307/591391]
FROW, J. (2005) On Literature in Cultural Studies. In M. BERUBE (Ed.), The Aesthetics of Cultural Studies (pp. 44-57). Malden, MA: Blackwell. [doi:://dx.doi.org/10.1002/9780470774182.ch2]
GILBERT, S. M., & GUBAR, S. (1979) The Mad Woman in the Attic: The Woman Writer and the Nineteenth-Century Literary Imagination. New Haven, Mass.: Yale University Press.
GOFFMAN, E. (1959). The Presentation of Self in Everyday Life. New York: Doubleday Anchor.
GOLDMANN, L. (1975) Towards a Sociology of the Novel (A. Sheridan, Trans.). London: Tavistock.
GOODHEART, E. (1999) Does Literary Studies Have a Future? Madison: The University of Wisconsin Press.
GORDON, C. (1980) Afterword. In C. Gordon (Ed.), Power/Knowledge (pp. 229-260). New York; London; Toronto Sydney; Tokyo; Singapore: Harvester Wheatsheaf.
GREENBLATT, S. (2005) Renaissance Self-fashioning: from More to Shakespeare. Chicago: University of Chicago Press.
GREENBLATT, S., & GUNN, G. (Eds.) (1992) Redrawing the Boundaries: The Transformation of English and American Literary Studies. New York: MLA.
GRISWOLD, W. (1993) Recent Moves in the Sociology of Literature. Annual Review of Sociology, vol. 19 pp. 455-467. [doi:://dx.doi.org/10.1146/annurev.so.19.080193.002323]
HABERMAS, J. (1984). The Theory of Communicative Action Vol. 1 (T. McCarthy, Trans.). Boston, MA: Beacon Press.
HACKING, I. (2004). Between Michel Foucault and Erving Goffman: between discourse in the abstract and face-to-face interaction. Economy and Society 33(3): 277-302. [doi:://dx.doi.org/10.1080/0308514042000225671]
HILFER, T. (2003) The New Hegemony in Literary Studies: Contradictions in Theory. Evanstone, Illinois: Northwestern University Press.
HILLS, M. (2002) Fan Cultures. London; New York: Routledge.
HOGGART, W. (1958) The Uses of Literacy. Harmondsworth: Penguin.
ISER, W. (1974) The Implied Reader : Patterns of Communication in Prose Fiction from Bunyan to Beckett. Baltimore: Johns Hopkins University Press.
ISER, W. (1978) The Act of Reading: A Theory of Aesthetic Response. Baltimore: Johns Hopkins University Press.
JAUSS, H. R. (1982) Toward an Aesthetic of Reception (T. Bahti, Trans.). Hemel Hempstead: Harvester Wheatsheaf.
JENKINS, H. (1992) Textual Poachers: Television Fans and Participatory Culture. New York: Routledge.
KENNEDY, D. (1979) Michel Foucault: The Archaeology and Sociology of Knowledge. Theory and Society, vol. 8, no. 2 pp. 269-290.
KERNAN, A. (1990) The Death of Literature. New Haven: Yale University Press.
KNORR-CETINA, K. (1981) The Manufacture of Knowledge: An Essay on the Constructivist and Contextual Nature of Science. Oxford: Penguin.
KNORR-CETINA, K. (1999) Epistemic cultures: how the sciences make knowledge. Cambridge, Massachusetts: Harvard University Press.
KUHN, T. S. (1970) The Structure of Scientific Revolutions (2nd ed.). Chicago: University of Chicago Press.
LATOUR, B., & WOOLGAR, S. (1986) Laboratory Life: The Construction of Scientific Facts. Princeton, New Jersey: Princeton University Press.
LATOUR, B. (1987). Science in Action: How to Follow Scientists and Engineers through Society. Cambridge, Massachusetts: Harvard University Press.
LAW, J. (1986) Editor's Introduction: Power/knowledge and the Dissolution of the Sociology of Knowledge. In J. Law (Ed.), Power, Action and Belief: A New Sociology of Knowledge. London: Routledge & Kegan Paul.
LAW, J. (2007) Actor Network Theory and Material Semiotics. <http://www.heterogeneities.net/publications/Law-ANTandMaterialSemiotics.pdf>, last accessed 9/10/2010.
LEAVIS, F. R. (1952) The Common Pursuit. Harmondsworth: Penguin Books.
LEMERT, C., & GILLAN, G. (1977). The New Alternative in Critical Sociology: Foucault's Discursive Analysis. Philosophy and Social Criticism, 4, 309-320.
LONG, E. (1985) The American Dream and the Popular Novel. Boston, Mass; London: Routledge & K. Paul.
LUKACS, G. (1971) The Theory of the Novel: A Historico-philosophical Essay on the Forms of Great Epic Literature (A. Bostock, Trans.). London: Merline Press.
MODLESKI, T. (2008) Loving with a Vengeance: Mass-produced Fantasies for woman (2nd ed.). New York: Routledge.
RADWAY, J. A. (1991) Reading the Romance: Women, Patriarchy and Popular Literature. Chapel Hill: University of North Carolina Press.
RADWAY, J. A. (1999) A Feeling for Books. Chapel Hill: University of North Carolina Press.
SACKS, O. (1970) The Man Who Mistook His Wife for a Hat. New York: Touchstone, Simon & Schuster.
SAID, E. W. (1978) Orientalism. London: Routledge.
SCHOLES, R. (1998) The Rise and Fall of English. New Haven; London: Yale University Press.
SCHWARTZ, R. B. (1997) After the Death of Literature. Carbondale and Edwardsville: Southern Illinois University Press.
SIMPSON, D. (1995) The Academic Postmodern and the Rule of Literature: A Report on Half-Knowledge. Chicago; London: University of Chicago Press.
SPIVAK, G. C. ([1992]1996) More on Power/Knowledge. In D. Landry & G. Maclean (Eds.), The Spivak Reader. New York; London: Routledge.
WILLIAMS, R. (1961) Culture and Society. Harmondsworth: Penguin Books.
WILLIAMS, R. (1977) Marxism and Literature. Oxford: Oxford University Press.
WILLIAMS, R. (1980) Problems in Materialism and Culture: Selected Essays. London: New Left Books.
WOLFF, J. (1999) Cultural Studies and the Sociology of Culture. Contemporary Sociology, vol. 28, no. 5 pp. 499-507. [doi:://dx.doi.org/10.2307/2654982]

