Paradoxes and Pitfalls in Using Fuzzy Set QCA: Illustrations from a Critical Review of a Study of Educational Inequality
by Barry Cooper and Judith Glaesser
Durham University; Durham University
Sociological Research Online, 16 (3) 8
<http://www.socresonline.org.uk/16/3/8.html>
10.5153/sro.2444
Received: 16 Jun 2011 Accepted: 10 Aug 2011 Published: 31 Aug 2011
Abstract
Charles Ragin's crisp set and fuzzy set Qualitative Comparative Analysis (csQCA and fsQCA) are being used by increasing numbers of social scientists interested in combining analytic rigour with case-based approaches. As with all techniques that become available in easy-to-use software packages, there is a danger that QCA will come to be used in a routinised manner, with not enough attention being paid to its particular strengths and weaknesses. Users of fsQCA in particular need to be very aware of particular problems that can arise when fuzzy logic lies behind their analyses. This paper aims to increase its readers' understanding of some of these problems and of some means by which they might be alleviated. We use a critical discussion of a recent paper by Freitag and Schlicht addressing social inequality in education in Germany as our vehicle. After summarising the substantive claims of the paper, we explain some key features of QCA. We subsequently discuss two main issues, (i) limited diversity and the various ways of using counterfactual reasoning to address it, and (ii) the logical paradoxes that can arise when using fsQCA. Making different choices than Freitag and Schlicht do in respect of dealing with these two issues, we undertake some reanalysis of their data, showing that their conclusions must be treated with some caution. We end by drawing some general lessons for users of QCA.
Keywords: Qualitative Comparative Analysis, FsQCA, Educational Inequality, German Educational Policy, Limited Diversity, Counterfactual Reasoning, Necessary and Sufficient Conditions, Case-Based Methods, Small n Methods, Fuzzy Logic
Introduction
1.1 We undertake a partial critical review of a recent paper (Freitag & Schlicht 2009) addressing a sociologically and politically important topic. Our main purpose, however, is not to provide a critique of this paper per se, but to use a critical discussion of it as a platform for exploring some important outstanding problems in fuzzy set configurational analysis (Ragin 2000, 2008) and how these might be addressed. We have several reasons for choosing this paper, which analyses the conditions and/or causes of differences in the degree of social inequality of educational access between German Länder, as our vehicle. First, the paper addresses a very important topic, making plausible and interesting claims about causes and policy options in an area where decisions impact on individuals' educational and occupational careers. Second, we believe that the authors, in reaching their conclusions, may have not considered as fully as they might have the complexities and paradoxes of fuzzy logical analysis. In addition, given that the techniques employed are not very well-known, readers need to be informed to a greater degree than they are in the authors' paper about some of the method-specific problems that need to be taken into account in judging the validity of the conclusions reached. Finally, Freitag and Schlicht have, very properly, made their procedure transparent, making it easy to reconstruct their methods and to reanalyse their data.Freitag and Schlicht's paper
2.1 Freitag and Schlicht's paper (2009) is a welcome addition to the literature on the meso-level causes of educational inequality. While systemic analysis of social inequality in educational outcomes is not new in itself, their use of Ragin's configurational analytic methods is innovative and welcome, given that the causes of differences between German Länder - their focus - are not likely to be simply linear in nature. Furthermore, while Ragin's Qualitative Comparative Analysis (QCA) has been employed in typological studies of welfare states (e.g. Kvist 2007), it has been used little, thus far, for similar purposes in the political sociology of education[1]. Ragin's set theoretic approach aims to provide an analysis of the necessary and/or sufficient conditions for some outcome. Freitag and Schlicht take this approach in analysing their German data, and make several strong causal claims and some policy recommendations.2.2 German secondary schooling is still mainly selective. Though comprehensive schools do exist in many Länder, in most there are still three main types of secondary school running from the most academic Gymnasium, via the Realschule, to the least academic Hauptschule, these existing alongside any comprehensive Gesamtschulen. Selection takes place at the end of primary schooling, though its timing, and the degree to which it can be modified, do vary across Länder. As possible causes of regional differences in inequality, Freitag and Schlicht focus on institutional differences between Länder in respect of the forms of secondary schooling, as well as differences in selection practices and the availability of pre-school education.
2.3 We will briefly summarise their complex paper. They develop their analyses and reach their conclusions as follows. Using a variety of data sources, they construct four "causal conditions" that vary across Länder[2]. All of these are expected, on theoretical grounds, to raise the likelihood of there being a high degree of social inequality in educational outcomes (measured by an odds ratio comparing access to the academically selective Gymnasium for children from different social backgrounds[3]). Their chosen four causal conditions characterising Länder, preceded here by their short names, are:
- CHILD: Underdeveloped Early Childhood Education
- FULL: Underdeveloped All-Day School
- SELECT: Strong Selectivity ("tripartition") in Secondary School Education
- TRACK: Early Tracking into Different School Types
2.4 These conditions are considered configurationally, i.e. instead of undertaking some form of regression analysis to determine the net effect of each factor, with others controlled, the authors employ set theoretic methods which focus on the ways in which conjunctions of these factors are, logically and/or causally, necessary and/or sufficient for there being high or low social inequality in educational outcomes. One key conclusion is that well-developed early childhood education is necessary for a low degree of educational inequality. They also make a number of claims about the conjunctions of conditions that are sufficient for both a high and a low degree of such inequality. These sufficiency claims are shown in Table 1, where upper case letters indicate the presence of a factor, lower case letters its absence, the * indicates that factors must be conjoined, and the + refers to logical OR, i.e. it indicates alternative paths to the outcome. It can be seen, for example, that CHILD, or "underdeveloped early childhood education", has been found to be a sufficient condition for high inequality. The single sufficient condition for low inequality is the conjunction of developed early childhood education and a low degree of early tracking.
| Table 1. Freitag's and Schlicht's main results |

|
2.5 We readily agree with the authors that QCA is a suitable tool with which to undertake a comparative analysis of the possible effects of structural and policy differences between the German Länder on the degree of social inequality of educational outcomes. However, the method is still under development, particularly in its fuzzy set theoretic form, and its use needs therefore to be accompanied by a high degree of methodological awareness if certain problematic aspects of fuzzy logical reasoning are to be avoided. We have struggled with some of these problems and paradoxes in our own work (Cooper & Glaesser 2008b). We will argue here that Freitag and Schlicht, in their analysis, have not taken full account of some of the problems that can arise in using fuzzy set Qualitative Comparative Analysis (fsQCA) and, as a result, their conclusions need to be treated with caution. In order to develop our argument we will need to discuss, in considerable detail, several features of fsQCA. In particular, without some understanding of the ways in which the "truth table algorithm" operates in fsQCA, of why some logically paradoxical results can arise, and the way "logical remainders" are dealt with by Freitag and Schlicht, readers will not be able to see exactly why and where possible problems in their analysis originate.
2.6 We will not, here, take the authors' decisions prior to their Boolean analysis of necessity and sufficiency as a matter for critical discussion. While others may want to question the particular choice they make of an outcome measure to represent inequality and of their putative causal conditions, and also their set theoretic calibration of these factors, we will not address these issues. Clearly, as with all analyses employing QCA, their results partly depend on these decisions (Ragin 2008). Our concern, though, is rather with some particular aspects of their analysis of their constructed and calibrated dataset. We believe these aspects need to be better understood by those employing fsQCA in the way the authors do, and by their readers.
2.7 The paper has the following structure. After introducing some key elements of QCA and fsQCA, in order to provide the necessary foundations for our later discussion, we use Freitag and Schlicht's core "truth table" to illustrate how such a table is constructed from fuzzy set data, concentrating not only on what such a truth table shows but also what it tends to hide from the less experienced reader. We then discuss, in turn, two central problem areas in the analysis of such truth tables, limited diversity and a key logical paradox that arises when fuzzy logic is employed, critically discussing the ways in which these have been handled by the authors. We then take account of our critical discussion in presenting some illustrative reanalyses of the truth table, showing why the conclusions drawn by the authors need to be treated with caution.
QCA: Exploring sufficiency with crisp and fuzzy sets
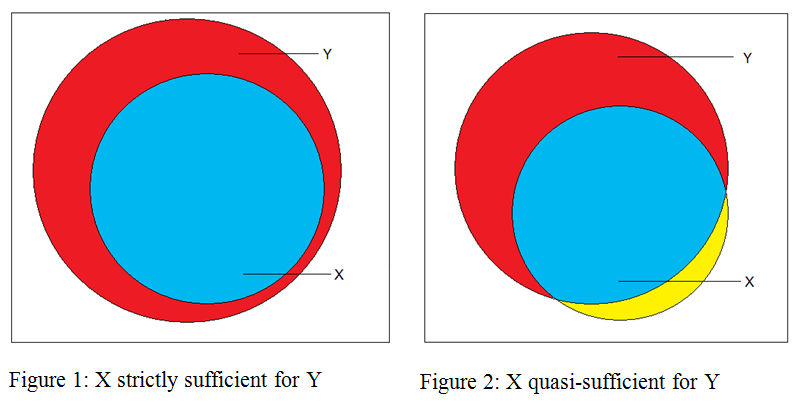
3.1 In order to develop our eventual argument, we need to present and discuss the way in which fsQCA, via its "truth table algorithm", produces its solutions, particularly for sufficiency. Taking the simple case of crisp sets first, where a case is simply either in or out of any set, then, for a condition, or a conjunction of conditions, X, to be strictly sufficient for an outcome Y, we need the set of cases with the condition, or conjunction of conditions, X, to be a subset of the set of cases with the outcome, as in the Venn diagram in Figure 1. Here, if X, then Y. More realistically, we will usually aim to test for quasi-sufficiency, as in Figure 2, where most, but not all, cases with the condition also have the outcome. Here, the proportion of the cases with X that also have Y can be used as a simple measure of the consistency of the subsethood relation with one of perfect sufficiency (Ragin 2006b), i.e. of the degree of approximation to perfect sufficiency.3.2 It can also be seen in these figures that not all cases of Y are "explained", or covered, by X. To capture this Ragin employs a measure termed "coverage" (analogous to "variance explained" in conventional approaches) which reports the proportion of the outcome set Y covered, or overlapped by, X. In these simple cases, this measure is equivalent to a measure of the degree of consistency with the necessity of X for Y. For X to be necessary for Y, Y must be a subset of X.
3.3 Crisp set QCA (developed by Ragin 1987) was criticised by some for employing dichotomous factors, though it is possible to use dummy variables as a way of avoiding some of the restrictions this imposes. However, since the publication of his 1987 book Ragin (2000, 2008) has worked to develop a fuzzy set based version of QCA, fsQCA, which allows configurational analysis to use continuous measures. Matters such as sufficiency become considerably more complicated when fuzzy sets are employed, where cases can have membership in the sets X and Y ranging from full non-membership of 0 through such values as 0.5 (as much in as out of a set) to full membership of 1.
|
3.4 The operations of conventional set theory (intersection, union, negation, subsethood, etc.) all have equivalents in fuzzy set theory (Goertz 2006, Ragin 2000, Smithson & Verkuilen 2006). To negate a fuzzy membership score, for example, one simply subtracts it from one. If a case has membership of 0.7 in a set, then it has a membership of 0.3 in the negation of this set. The simplest way of assessing fuzzy subsethood uses an arithmetic approach. If the membership of a case in set X is arithmetically less than or equal to its membership in set Y, then this case passes the test for fuzzy subsethood (also called fuzzy inclusion). On a plot of membership in Y against membership in X, such cases are on or above the Y=X line, i.e. they comprise an upper triangular plot (Ragin 2008, p. 48). The proportion of cases with non-zero membership in the condition set X passing such a test can be used as a simple test of consistency with a relationship of sufficiency for some outcome set Y, i.e. of the degree to which perfect sufficiency is approximated[4]. This simple approach is not, however, the one implemented in fsQCA's "truth table algorithm". We will briefly explain the principles behind the alternative that is actually implemented in the software (Ragin et al. 2008).
3.5 Looking at Figure 2, it can be seen that, for crisp sets, the proportional measure of consistency with sufficiency actually is equivalent to comparing the size of two sets, one the intersection of the sets of cases with X and Y (blue subset), the other the set of cases with the "causal" condition X (the blue and yellow subsets taken together). In set theoretic terms, this measure of the degree of consistency with sufficiency[5], for crisp sets, is:
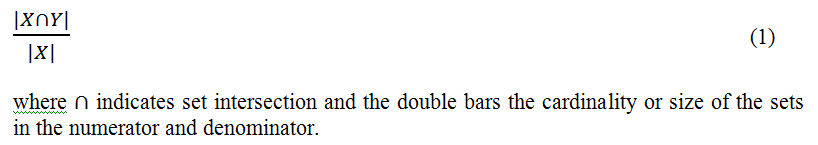
3.6 The procedure implemented in fsQCA's "truth table algorithm" uses a fuzzy set analogue of this expression. In the crisp set context, we get our measure of the size of a set by simply counting the number of members in it. Clearly simple whole number counting won't work for a fuzzy set, where cases can have partial membership. However, an "obvious" intuitive measure of the size of a fuzzy set is given by summing the partial membership for all cases in a set. Formally, if mx represents the degree of membership of each case i in the set x, a measure of the size of x is given, if we sum over all the members i of the set, by:

3.7 This provides us with a "fuzzy" way of calculating the denominator of expression (1). To calculate the numerator, we need, in addition, a fuzzy analogue of crisp set intersection. The operation employed in fsQCA for the intersection of two (or more) fuzzy sets involves taking the minimum of the cases' membership in each set. Taking this approach (see Ragin 2006b), we have, for evaluating the fuzzy set sufficiency of x for y, the following expression for the consistency of the relation with one of sufficiency, where the intersection in the numerator is operationalised as the minimum of mx and my for each case[6]:

Constructing a truth table with fuzzy sets
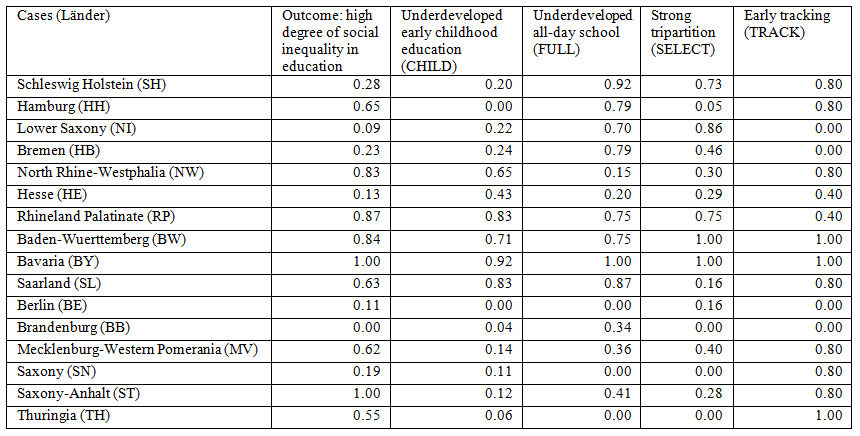
4.1 We now need to consider how these definitions and procedures allow the construction of a "truth table" from fuzzy set data. In doing so, we move from considering a condition X to considering conditions comprised of combinations of factors. The truth table plays a crucial role in QCA by summarising the relations between sets representing configurations of conditions and the presence or absence of the outcome under study. What is involved in moving from a fuzzily calibrated dataset to a truth table ready for analysis can be illustrated by looking at two tables from Freitag and Schlicht's paper. Table 2 shows the fuzzy scores they allocated for each German Land to the outcome and the four conditions. Table 3 is their resulting truth table. With four "causal" conditions, a truth table will have 16 (i.e. 2 to the power of 4) rows.| Table 2. the fuzzy membership scores for the properties of Länder (from Table 3 of Freitag & Schlicht's paper) |
|
| Table 3. Freitag and Schlicht's truth table |

|
Note (to the original table): The columns in grey boxes indicate the results are judged as consistently sufficient for the outcome. The columns in white boxes indicate logical remainders [that] are included in the reduction for the most parsimonious solution (quoted from Freitag and Schlicht, p. 60).
4.2 We can use use the case of Hamburg (HH) to explain exactly how a case is allocated to just one row of the truth table (Table 3). Hamburg has these values for the conditions:

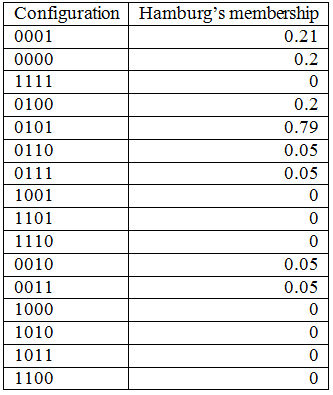
4.3 Consider the first row of Table 3, marked as the configuration 0001. This can be spelt out more fully, using the upper and lower case notation, as child*full*select*TRACK. What degree of membership does Hamburg have in this configuration? To calculate this we must first negate three conditions (the 0s) and then take the minimum (for set intersection) of these membership values and the score for TRACK. Doing this requires us to calculate the MINIMUM [ (1-0), (1-0.79), (1-0.05), (0.80) ] which reduces to MINIMUM [ (1), (0.21), (0.95), (0.80) ], giving a membership for Hamburg of 0.21 in child*full*select*TRACK. These rules for negation and intersection generate the memberships for Hamburg in the 16 configurations shown in Table 4.
| Table 4. Hamburg’s membership in the 16 configurations |
|
4.4 Inspection of these shows that Hamburg has non-zero membership in half of the 16 logically possible configurations, but passes the value of 0.5 indicating that it is more in than out of the configuration in just one case, that of 0101 or child*FULL*select*TRACK[7]. As can be seen from Table 3, Hamburg (HH) is allocated to this row in which it has its greatest membership. The remaining Länder are allocated in the same way. It can be seen that six configurations have no cases with memberships of over 0.5 though, as will become important for our arguments later, they do have cases with smaller memberships. We will call cases with membership of greater than 0.5 "good" cases for the configuration in which they have this membership. Six configurations have no such "good" cases. It is clearly important, given this complexity, to understand both what a truth table derived from fuzzy sets shows and what it hides. As we explained earlier, in discussing Hamburg, the use of 0s and 1s should not be taken here, as they should be in truth tables derived from crisp sets, to indicate that the four Länder shown against 0001 actually have scores of 0 or 1 in the four conditions. The configuration 0001 rather represents an ideal type (Kvist 2007), or the corners of the cell in a 4-dimensional vector space in which these four Länder have their greatest membership.
4.5 Before returning to the discussion of consistency, we'll just note some important features of this particular truth table. First, in Table 5 we show the actual membership values that each Land has in the configuration against which it appears in the truth table. This shows for example that, if we look at the two Länder that appear in the row 1111 (CHILD*FULL*SELECT*TRACK), BW and BY, their scores are 0.71 and 0.92. They are both "good" cases (> 0.5) but we can see that they are not equally "good" and also that the score of 0.71 for BW would only be associated with the verbal description "more or less in the set" by Ragin himself (2000). If we examine all the Länder, looking at their membership in their allocated configuration (Table 5), we can see that some are not such good exemplars of their configurationally defined type of case as these two. Three cases, ST, HE and HB, have largest memberships of 0.59, 0.57 and 0.54 respectively, values very close to the 0.5 point representing being as much in as out of the set. These are not very "good" cases of their type.
| Table 5. Highest membership of Länder in any configuration |
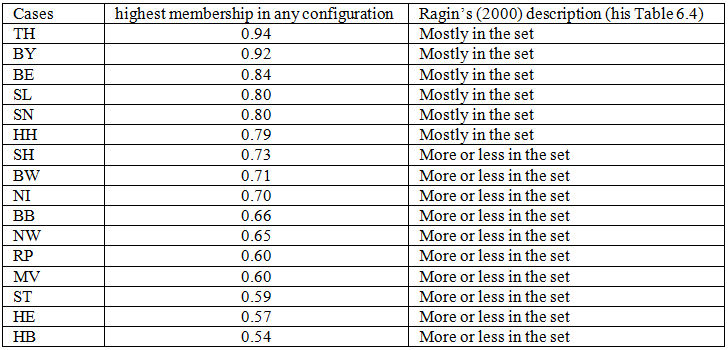
|
4.6 Another important point concerns the rows that have no "good" cases. As we explained earlier, some Länder will have partial memberships, lower than 0.5, in these configurations. As an example, consider the row 1100, i.e. CHILD*FULL*select*track. Table 6 shows the membership of all the Länder in this configuration. Ten cases have non-zero membership, but all are lower than 0.5, as expected, and the highest, RP, has just 0.25. Some implications of this will be discussed later.
| Table 6. Membership values of the Länder in the configuration 1100 |

|
Consistency again
5.1 We return now to consistency. We can see the results of expression (3) for calculating consistency being used in practice by looking at Table 3. Taking the first row, 0001, as an example, we have here the configuration or type, using the lower and upper case notation employed by Freitag and Schlicht, child*full*select*TRACK. The "good" cases, i.e. Länder, falling under this type are shown (see Table 2 for their full names) and, crucially, in the final two columns, the consistency with a relationship of sufficiency for this configuration is shown for both the outcome and its negation. Using expression (3), and letting x be, in turn, each configuration represented by the rows of the table, while y is taken, first, to be the outcome of a high degree and then, second, the outcome of a low degree of social inequality in education, Freitag and Schlicht obtain the complete set of consistencies with a relation of sufficiency shown in the final two columns. These two figures are, then, an assessment of the degree to which each configuration, treated as a fuzzy set, is, respectively, a subset of the fuzzy set for the outcome or the negated outcome.5.2 It should be stressed, however, that these consistencies are calculated using not just the "good" cases that appear against each row but by using all the non-zero memberships that Länder have in any row (hence the appearance of consistencies for rows that have no "good" cases[8]). Contrary to this, many might have expected consistencies to be calculated using only "good" cases (resulting in rows with no "good" cases having no consistency figures). Ragin himself (2008, 129-130) has chosen to use all cases with non-zero membership to calculate consistency, this following from a concern with the overall relationship of fuzzy subsethood between any configuration of conditions and the outcome, while he uses the number of cases in a configuration with membership of over 0.5 to give a separate indication of whether there are "good" cases exemplifying this relationship. We will return to some paradoxical results this choice produces, given the distribution of membership values in the authors' calibrated dataset, later[9].
5.3 Having provided the necessary background, we now discuss the two key interrelated problems that arise in the analysis of Freitag and Schlicht's truth table. These problems concern (i) how to address the "limited diversity" that characterises this (and many other) truth tables and (ii) a logical paradox that arises when consistencies are calculated using fuzzy membership data for all cases with non-zero membership, i.e. not just "good" cases. After discussing these two issues we will undertake some reanalysis of the truth table to show how different ways of responding to these problems than Freitag and Schlicht's preferred approach leads to different conclusions from theirs.
Limited Diversity
6.1 Ragin has stressed that data taken from the social world are often characterised by limited diversity. By this he refers to the fact that, especially given small to medium size samples or populations, some configurations of factors are likely to be represented by few or even no cases. In his more recent writings (e.g. 2008), he has recommended various forms of counterfactual reasoning as a fruitful way of addressing the problems such limited diversity produces for the analyst wishing to produce configurational accounts of the sufficient and/or necessary conditions for some outcome. Table 3 here shows such limited diversity. Considering just "good" cases, the sixteen Länder do not, as the authors themselves note, cover, the sixteen possible configurations or types. As we explained above, while there are four "good" cases of Länder available to represent the type appearing in the first row, 0001, there are none at all to represent any of the six appearing in the bottom rows of the table. Such rows, lacking any "good" cases at all, are termed "logical remainders" in the QCA literature (Ragin 2008, 131-133).6.2 This high degree of limited diversity has the consequence, in the context of the empirical distribution of the cases that do exist across the various conjunctions of conditions and the outcome, that any set theoretic accounts of the combinations of the conditions sufficient for the outcomes of high or low inequality will tend to be complex rather than parsimonious in form (Ragin 2008), as will be seen later. The authors do include such complex solutions in their footnotes, but choose to avoid focusing on them in the body of their text, discussing instead, and drawing their conclusions from, some more parsimonious solutions that have been produced by making various counterfactual assumptions about what the outcomes would have been, had suitable cases actually existed, for the "remainder" configurations lacking "good" empirical cases. We will raise some concerns about the way these decisions have been made.
6.3 To follow our argument here one needs to understand what happens to the rows of a truth table during the process of minimisation that the fsQCA software uses to produce its solutions. We can take the "complex" rather than "parsimonious" analysis of the sufficient conditions for a high degree of inequality as an example, using just rows that have at least one "good" case. Here "logical remainder" rows, whatever their consistency figures, are not allowed into the minimised solution of the truth table. The penultimate column of Table 3 provides the relevant consistency figures. None of these reach the figure of 1.0 that would indicate a configuration is strictly sufficient for the outcome, but several do reach quite high values, such as 0.9 or 0.98. The analyst must set a threshold figure for the lowest consistency value which will be taken to indicate the quasi-sufficiency of a configuration for the outcome. It is conventional to take account of any large gaps in the distribution of consistency values across configurations in making this decision. The authors choose, for their analysis, a value of 0.85. Of the ten rows with "good" cases, five pass this test. They are, using the 0/1 notation: 1111, 0101, 1110, 1101 and 1001. These include six of the sixteen "good" cases in Table 3[10]. This solution for quasi-sufficiency could be written, using the 0/1 notation, as:
1111 + 0101 + 1110 +1101 + 1001.
6.4 In fsQCA practice, however, the next step is the minimisation of this complexity, with the goal of producing, if possible, a simplified expression. The minimisation process is simple in principle if not in practice. Take, for example, the two configurations 1111 and 1101, both of which have passed the test set for quasi-sufficiency. It can be seen that the third factor, strong selectivity, makes no relevant difference, given the chosen level of consistency. These two terms can be collapsed to 11-1 where the dash indicates that the third factor makes no difference. Using repeated applications of such a procedure fsQCA produces minimised overall solutions of such dichotomised truth tables as Table 3. The resulting minimised "complex" solution is:
CHILD*select*TRACK + FULL*select*TRACK + CHILD*FULL*SELECT.
6.5 Readers new to QCA might have expected only the five rows meeting the chosen consistency threshold of 0.85 and having at least one "good" case to go forward into a minimised solution. On this view, rows with no "good" cases should not enter the minimisation process, with the solution remaining the "complex" one just given. Ragin (2008) has argued, however, that there are situations where our theoretical knowledge, independently of the consistency scores for "logical remainders", can justify making counterfactual assumptions as to whether some other configurations, from amongst those lacking "good" or even any cases, would be quasi-sufficient for the outcome to occur. Allowing such additional counterfactual configurations into the minimisation process can provide simpler and more general overall solutions. Crucially, in addition to this theoretically driven approach, an alternative possibility is just to allow the software, in a less theoretically informed way, to allocate the outcome or its absence to these logical remainder rows in whatever way produces the most parsimonious minimised solution. Here remainder rows are treated as "don't cares' in fsQCA. Freitag and Schlicht opt for this atheoretical, and rather mechanical, parsimonious approach, providing some justificatory argument after the event.
6.6 Table 7 gives the full details[11] of the complex solution[12] (4) for a high degree of social inequality, i.e. the solution that allows only the five rows having "good" cases and passing the threshold to go forward, setting it against the parsimonious solution (5) preferred by the authors, this being:
CHILD + FULL*select*TRACK.
6.7 In both cases, these expressions show the combinations of the presence or absence of four causal conditions that are quasi-sufficient, at the chosen 0.85 consistency level, for this outcome. The key point concerning solution (5) is that, in addition to the five configurations that actually have "good" empirical cases in the dataset, it contains four other configurations that have no such "good" cases. These are the four configurations sitting at the bottom of Table 3, one of which we discussed in an earlier section. In producing this parsimonious solution, the authors have added nearly as many logical remainders to the solution (four) as they have configurations with actual "good" cases (five). The added rows are those boxed in Table 3, being 1000, 1010, 1011 and 1100. These are now all included in the minimised solution as subsets of CHILD.
| Table 7. Complex and parsimonious solutions for the outcome, high degree of social inequality in education |

|
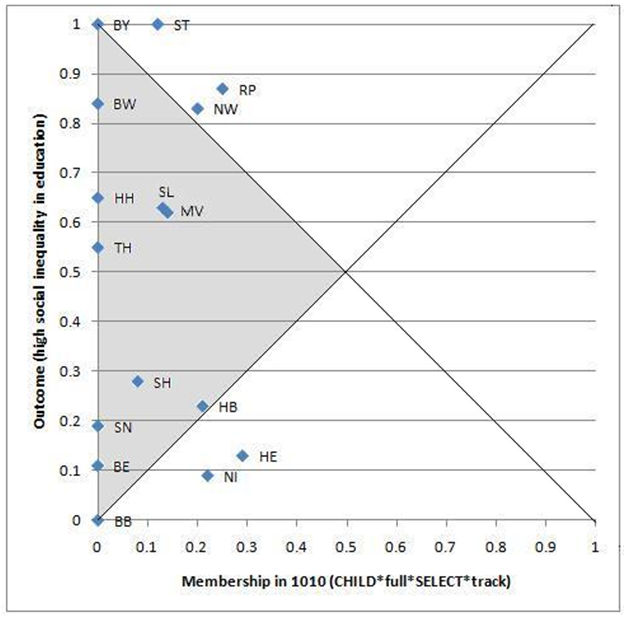
6.8 What then precisely underlies the conclusion that underdeveloped early childhood education is sufficient for a high degree of social inequality? We can explore this, illustratively, by examining a configuration that is claimed under expression (5) to be sufficient, but is a logical remainder, i.e. one that has no "good" cases. Consider the configuration, 1010, for which there are no "good" cases. This does happen to have a consistency of 0.82, approaching the threshold of 0.85. This is not, however, the reason it has been included in the solution (as a subset of CHILD, i.e. of 1- - -). It has been included simply because allocating to it, counterfactually, the outcome rather than its absence produces a more parsimonious solution. It might be argued, however, that the near to 0.85 consistency figure could be used to lend support to this particular decision. The plot of the fuzzy membership scores for the outcome, a high degree of social inequality in education, and for this configuration, CHILD*full*SELECT*track, are shown in Figure 3.
6.9 Of the sixteen cases, seven have no membership at all in this conjunction of conditions. Of the nine remaining cases, seven fall into the upper triangular area of the plot, thereby formally satisfying the simple x= <y condition for sufficiency. However, amongst these nine cases, the highest membership in 1010 is 0.29. This set of partial memberships seems a very weak basis for allowing the configuration 1010 to be taken forward into the minimisation procedure, whether this decision is based on increasing parsimony (since there are actually no good cases of German Länder of this type) or on the near to 0.85 consistency figure. A similar point applies to the other three remainders that have been allowed to go forward. The highest memberships of any Länder in them are, in turn, 0.25 for 1100, 0.3 for 1011 and a larger 0.43 for 1000 (though the next largest value is only 0.25).
6.10 In relation to possibly taking account of the consistency figures for remainder rows, Ragin, notwithstanding his decision to calculate consistencies in the "truth table algorithm" on the basis of all cases having non-zero membership, however small, in the condition set, has raised some relevant concerns about relying on such cases:
Imagine trying to support an argument in an oral presentation to colleagues using in-depth evidence on a case with only weak membership in the relevant sets. The common sense thinking that indicates that this presentation would be a waste of time is precisely formalized in fuzzy membership scores. Cases with strong membership in the causal condition provide the most relevant consistent cases and the most relevant inconsistent cases. (Ragin 2008, pp. 49-50) [13]
6.11 We have come to believe this argument has much to recommend it and have taken it into account in determining the nature of the illustrative reanalyses we will present later in the paper. However, for anyone contemplating using the consistencies associated with remainder rows in place of purely mechanical considerations of parsimony to determine which remainders are allocated the outcome, there is a further specific problem arising from reliance on cases with small memberships in calculating consistencies – that of logical paradoxes. We consider this next.
Paradoxical results with fuzzy sets
7.1 Here we discuss certain paradoxical results that can result from the use of fuzzy sets and logic, of which any analyst needs to be aware. It is, of course, a feature of fuzzy sets that a case can have membership in both a set and its negation, with the latter being calculated by subtracting the membership score in the first set from 1. If a case has membership in X of 0.3 and membership in Y of, say, 0.6, then we can see that X will be found to be sufficient for Y, since X is less than or equal to Y. However, X is also sufficient for NOT-Y (i.e. 0.4, derived from 1.0 minus 0.6), since X is less than or equal to 0.4[14]. Given, then, the use of fuzzy sets and logic, a situation can arise where the same configuration can be quasi-sufficient for an outcome and its negation, a worrying situation from the perspective of causal analysis.
|
| Figure 3. outcome by 1010 (consistency is 0.82) |
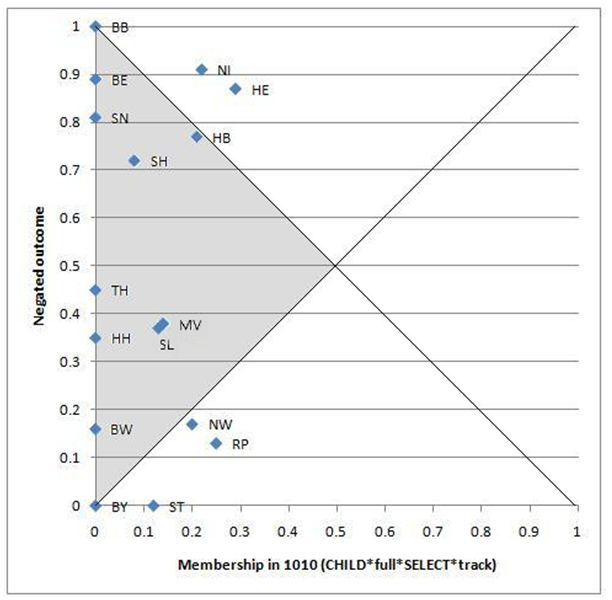
7.2 Depending on exactly where the threshold is set, we can find examples of this in Table 3. For example, the consistency values for the outcome, high degree of social inequality of education and its negation, for the configuration 1100, are 0.9 and 0.86. The authors have chosen to use a mechanical parsimony-seeking approach to allocate the outcome or its absence to the remainder rows, i.e. they do not pay attention to the consistency figures that appear next to these rows. We can see, however, that the consistency figures, in some cases, are not in line with the results of the mechanical approach. For example, in the case of the configuration 1010, which they have, as we saw above, allowed to go forward as part of the solution for high inequality, the consistency figure, based entirely on "not good" cases, is actually slightly larger for the negated outcome, i.e. low inequality (0.84 compared to 0.82). This might seem to be another reason for them to reconsider the minimised solution that has incorporated 1010. Not only, as we showed in the last section, does it lack "good" cases, but, in addition, it is more strongly quasi-sufficient for the negated than the non-negated outcome. The same point applies, more strongly in fact, to 1000 (with 0.85 for the negated outcome compared to 0.79 for the outcome). The authors appear to have privileged parsimony over such alternative considerations. However, it turns out that the paradoxical results that arise when consistencies are based on low scoring cases would themselves raise problems for any alternative approach which takes the consistencies for the remainder rows into account.
7.3 We will now explain the relationship between low scoring cases and the appearance of paradoxical results. Figure 4 shows the scatter of cases for membership in the negated outcome (what the authors term low social inequality) by membership in the configuration 1010. In both this graph and that in Figure 3 for the outcome of high inequality, we have shaded the region where paradoxical results arise[15].
|
| Figure 4. Negated outcome by 1010 (consistency is 0.84) |
7.4 For this configuration, 1010, which has, paradoxically, a consistency with the outcome of 0.82 and with the negated outcome of 0.84, it is easy to see that the reliance on low-scoring cases has produced the paradoxical result that 1010 tends to quasi-sufficiency for both high and low inequality. Ignoring the 7 cases where the fuzzy score for the configuration is zero (which contribute nothing to the consistency score), we can see that, in each graph, 4 of the remaining 9 cases fall into the "paradoxical" region (and the others are near it), explaining, given the rather symmetrical distribution of the cases as a whole around the y=0.5 line, the two similar consistency scores. Clearly, if, instead of using the parsimony-seeking approach to determine which remainder rows enter a solution, a researcher were to turn to the consistency figures associated with these rows, the danger of paradoxical results would immediately become a major problem to address. Both approaches, that of parsimony-seeking and that depending on consistency scores derived from only "non-good" cases, are problematic. The root cause is the same: the absence of "good" empirical cases for these rows.
Some reanalyses
8.1 We now explore what difference it makes to the authors' conclusions if we take some of our concerns into account in carrying out a reanalysis of their truth table. There are several things we could do, apart from the most conservative decision of accepting the complex solution (4) in Table 7 and the corresponding complex solution for the negated outcome. First, in place of the mechanical parsimonious approach we might use Ragin's (2008) more theoretical approach to counterfactuals to allow some remainders to be incorporated as "easy" counterfactuals into the minimised solution. In doing this, we might or might not take account of the consistency figures that appear in Table 3 for these remainder rows[16]. In doing this, we would be creating an "intermediate" solution falling somewhere between the bounds set by the complex and parsimonious solutions in Table 7. Second, we could use the additional alternative measure for consistency that has appeared in recent revisions of the fsQCA software (the PRI measure). This measure is designed to remove the contribution of cases that fall into the paradoxical region, but its properties are not yet, to our knowledge, well understood. Third, we could run some analyses that only employ data for good cases, i.e. those with membership over 0.5 in each row. These possibilities serve to remind us how much judgement needs to be used in order to produce valid analyses when fuzzy sets are employed[17].8.2 Given the limitations of space, we'll take, as our illustration, the third possibility, looking at what happens if we use just the "good" cases to calculate the consistencies that determine, once a threshold is set, which rows go forward into any minimised solution[18]. We will show that this also, like Ragin's recent PRI measure, addresses, to some extent, the problem of paradoxical consistencies arising for the outcome and its negation. However, given Ragin's own recent arguments for preferring intermediate solutions[19] (Mendel & Ragin 2011), we will also, within the context of our using just "good" cases, say a little about the use of counterfactual reasoning and parsimony.
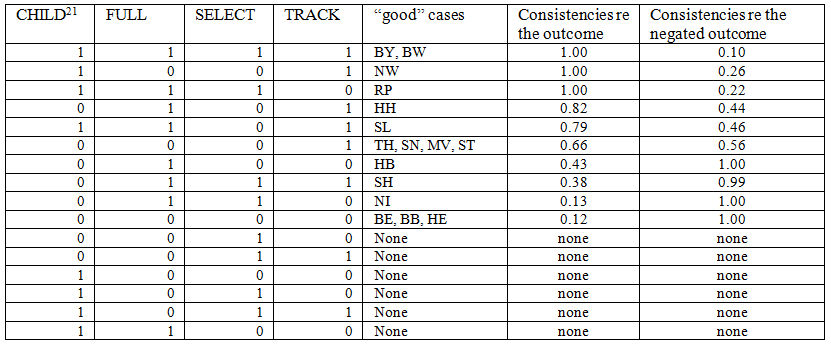
8.3 Taking, first, this "good" cases route, and using expression (3) to calculate consistencies, produces the revised truth table for sufficiency shown in Table 8 (where, of course, some rows have no "good" cases and, hence, now, no consistencies).
8.4 We can see, by examining the pairs of consistency figures for the outcome and its negation, that the paradoxical results that characterised Table 3 have mainly disappeared. For example, while in Table 3 we had, for 0111, the two values 0.79 and 0.78, we now have 0.38 and 0.99. This configuration is now clearly sufficient for the negated outcome and clearly not so for the outcome. The one configuration where the two values remain close is 0001. This reduction of paradoxical results is a major benefit of using just "good" cases to set against the disadvantage of losing some of the evidence relevant to subset relationships that might be derived from using cases with low memberships in rows without "good" cases.
8.5 We can proceed to minimise this truth table, starting with the complex solution for the outcome, high social inequality in education. Taking account of jumps in the consistencies, two obvious thresholds present themselves, 1.0 and 0.75. To keep our argument simpler we will just concentrate on the expressions that appear in the solutions for quasi-sufficiency, which we wish to compare with those derived by Freitag and Schlicht, and will ignore the details of coverage. We obtain the minimised solutions shown in Table 9 under "complex solutions". We have used the lower threshold of 0.75 partly, as we said, in recognition of a jump in the consistency figures, but also in order to note that this solution reproduces the authors' own complex solution with a threshold of 0.85 (see their footnote 17). It is not, of course, the same as their favoured parsimonious solution (see Table 1 here) which was CHILD + FULL*select*TRACK. A plot of our 0.75 complex "good" cases solution is shown in Figure 5[20]. If we were to plot our 1.0 complex solution, CHILD*FULL*SELECT+ CHILD*full*select*TRACK, we would lose the two cases, HH and SL, below the y=x line.
| Table 8. Truth table with consistencies based only on "good" cases |
|
8.6 Given that, including just "good" cases, a minimised solution using the authors' threshold of 0.85 would generate the solution CHILD*FULL*SELECT+ CHILD*full*select*TRACK and that our second "good" cases analysis, employing 0.75, has generated the authors' complex rather than their favoured parsimonious solution, we would argue that their conclusions need reconsideration. However, our main point has not been to question the particular conclusions of Freitag and Schlicht but rather to explore the working assumptions, some of which seem to be open to question, that underlie them in order to increase users' understanding of the complexities of fuzzy logical analysis.
| Table 9. Sufficiency (for outcome of high inequality) using just "good" cases |

|
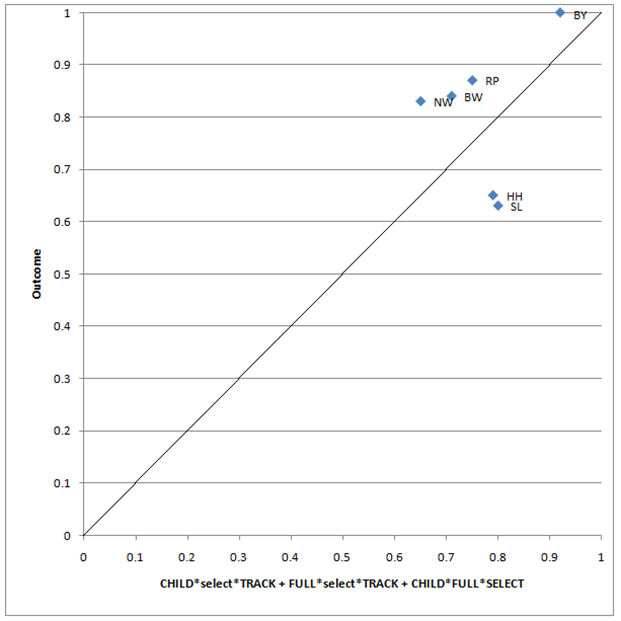
|
| Figure 5. The outcome by the solution CHILD*select*TRACK + FULL*select*TRACK+ CHILD*FULL*SELECT |
8.7 We can push this concern further by showing how, in the face of limited diversity, different treatment of the six "remainder" rows generates the three different solutions of a truth table that fsQCA allows. The complex solution allows no remainders to be included in the minimisation[22]. The parsimonious solution, as explained earlier, allows remainders to be allocated atheoretically, simply in the interests of the simplest possible solution[23]. The intermediate solution is derived by taking account of theoretically derived assumptions entered by the analyst concerning the expected direction of the effects of some or all factors[24]. The latter requires us to understand what Ragin means by counterfactual reasoning. In Table 8 we can see that the configuration 1001 is sufficient for the outcome. There are two "remainder" configurations, 1101 and 1011, which differ from this on one condition but for which we have no "good" cases. In each of these one 0 is changed, in comparison with 1001, to a 1, introducing the presence of a factor assumed by Freitag and Schlicht, theoretically, to contribute to the outcome. The researcher might argue that if 1001 is sufficient for high inequality then it is reasonable to assume that, were cases of 1101 and 1011 to exist, then we would find these configurations also to be sufficient. Therefore s/he could choose to allow these two remainder rows to go forward into the solution. The "intermediate" solutions in Table 9 have been generated by entering four such assumptions, i.e. that adding the presence in such pair-wise comparisons of any of CHILD, FULL, TRACK and SELECT will tend to increase inequality. On the other hand, as explained earlier, the "parsimonious" solutions have been produced by allowing the software to allocate the outcome or its absence to these logical remainder rows in whatever way produces the most parsimonious solution. We would just note that the intermediate solutions generate yet another argument for the use of judgement. They differ both from our "complex" solution based on "good" cases as well as from the solutions favoured by Freitag and Schlicht.
8.8 What about the negated outcome (termed by the authors "low inequality")? Our revised results, based on just "good" cases, are shown in Table 10. Here, again, we have generated three minimised solutions by treating remainders differently. In producing the intermediate solution, we have assumed that the absence of each of CHILD, FULL, TRACK and SELECT will tend to reduce inequality. In the case of the parsimonious solution, a further complication arises, given that there are two possible minimisations of the truth table (see Table 10).
| Table 10. Sufficiency (for outcome of low inequality) using just "good" cases |

|
8.9 The parsimonious solution given by the authors is simply child*track[25]. None of our three "good" case solutions matches this. Once again, we are faced with making choices between solutions based on different working assumptions. It is not clear why we should prefer the parsimonious solution chosen by Freitag and Schlicht.
Concluding remarks
9.1 Freitag and Schlicht present their conclusions in a fairly confident manner; for example:
Altogether, we have provided a scientific foundation to the lively debate about the causes of highly differential degrees of social inequality in education among political units. Our results mainly indicate the relevance of early childhood education for the existence of social inequality in education. As we hypothesized, availability of early childhood education seems to be able to mitigate different preconditions of starting school. An absence of both, widely available early child care and high preschool enrollment rates, is sufficient for a high degree of social inequality in education. (p. 66)Our discussion suggests that they should be more circumspect.
9.2 What are the main lessons of our discussion? There are several to stress. Clearly, in general, all analytic techniques need to be used in conjunction with judgement and an understanding of the main likely threats to valid analysis likely to arise in their use. It is especially important to report these threats explicitly when, as with fsQCA, mathematics such as fuzzy sets and logic, whose properties are new to most social scientists, are embedded in easily available and easy-to-use software. More particularly, when using fsQCA in the context of limited diversity, there are potential counterfactual decisions over logical remainders to be made which will be, and will remain, contestable. Ragin (e.g. 2008) has argued the need for care in this area. Any researcher not wishing to report only the complex solution of his or her truth table will need to turn to counterfactual reasoning about logical remainders. Such reasoning will only be as good as extant theory[26].
9.3 Having noted the difficulties that will arise in using contestable counterfactual reasoning, we would still, in general, want to argue against the mechanical approach employed in producing the parsimonious solutions favoured in Freitag and Schlicht's paper. We can understand why Ragin has expressed a preference for intermediate solutions in his recent dialogue with Mendel (Mendel & Ragin 2011), especially given the frequency with which QCA has been used with small datasets that give rise to limited diversity. Our own current view is that, except where a very strong body of existing theory can provide a sound basis for the counterfactual reasoning that allows some logical remainders into solutions, it might be safer to privilege complex solutions.
9.4 Against this position, it can be pointed out that complex solutions effectively assume that any remainder rows do not obtain the outcome, i.e. that, in terms of Boolean logic, they are "false" (e.g. Ragin 2000, p. 106). This certainly means that the complex solution might not contain all the configurations that are really sufficient for the outcome (and this would then prevent some simplification of the solution). However, whether, in any particular analysis, this implicit assumption of "falsity" for the remainders is accepted by default or not, those configurations reported as sufficient for the outcome in the complex solution remain so, since they would still appear as a subset of any more general solution that incorporated some remainder rows as "true". What is lost, if the default assumption concerning remainders is false, is the chance to declare that, for example, A*B is sufficient for the outcome rather than A*B*c (or, alternatively, A*B*C). Now, whether this matters seems to us to depend on whether it is thought that A*B*c and A*B*C are causally equivalent or not (i.e. whether A*B does or does not collapse two combinations sufficient for the outcome that actually are different at the level of mechanisms and processes). This points to a general issue re minimisation that deserves more discussion.
9.5 More mundanely, on the basis of what we have explored in this paper, we would recommend that researchers always look carefully at fuzzy scatterplots of outcomes and negated outcomes by membership in the configurations that comprise the truth table (see our Figures 3 and 4). This should focus attention on the proportion of their cases that fall into the paradox-generating region. The effects of a large proportion of cases falling here should also be visible in the truth table columns for consistency for the outcome and its negation, as they were here in Table 3. We would also recommend that researchers consider running parallel "good" case analyses, as we have, since these can act as a useful check on the likely validity of analyses that employ all cases[27].
Acknowledgements
An earlier version of this paper was presented at methods@plymouth in May 2011. We’d like to thank the participants for their comments and questions. We’d also like to thank Martyn Hammersley, Charles Ragin, Raphaela Schlicht and Stephanie Thomson for their comments on that version. All responsibility for any errors remains ours. This work was supported by an Economic and Social Research Council (ESRC) research fellowship [RES-063-27-0240] awarded to JG.
Notes
1 It has been used for micro-sociological purposes in this field. See Cooper (2005a,b), Cooper & Glaesser (2008a,b, 2010, 2011), Cooper & Harries (2009), Glaesser (2008), Glaesser & Cooper (2010), Ragin (2006a).2 They also employ some other measures as controls in further analyses, but little detail is given, and we will not discuss these here.
3 We quote: "The odds ratios represent the varying chances of being enrolled at the Gymnasium, as opposed to one of the other school types, for the highest and second-lowest (reference quartile in PISA-E, working class) ESCS quartiles" (Freitag and Schlicht, 2009, p. 51).
4 For an example of this approach in use, see Cooper & Glaesser (2010) and, for a discussion of some of its disadvantages, chapter 5 of Cooper, Glaesser, Hammersley and Gomm (in press).
5 The parallel expression for coverage replaces |X| with |Y|.
6 This expression gives the conventional result for two crisp sets since, there, the two summations reduce to counting the members of the sets. The parallel expression for fuzzy coverage replaces, in the denominator, the sum of the memberships in x with those in y.
7 A case will always have membership of 0.5 or larger in at least one configuration. A case will never appear in more than one configuration with a membership larger than 0.5. There are circumstances, however, where a case will not appear in any configuration with a membership over 0.5. This arises when the case has a membership in at least one of the condition sets of exactly 0.5. For example, with four conditions, as we have here, if a case were to have membership in the sets of 0.5, 0.3, 0.6 and 0.7, then its highest membership in any configuration would be 0.5 (which it would have in two of the 16 configurations).
8 It is always possible to calculate consistencies for rows with no "good" cases, just as long as there are some cases with non-zero membership in these rows.
9 We should note that Ragin, having reflected over a long period on this choice, is well aware of its pros and cons in comparison with the alternatives (as will become clearer later).
10 There are, incidentally, nine Länder which are "good" cases of high inequality, i.e. which have a membership of over 0.5 in this fuzzy outcome set (Table 2).
11 For an account of raw and unique coverage, see Ragin (2006b).
12 See footnote 17 of Freitag and Schlicht (2009).
13 In Ragin (2005, p. 8) he made a similar point: "The distribution of cases across causal combinations is easy to assess when causal conditions are represented with crisp sets, for it is a simple matter to construct a truth table from such data and to examine the number of cases crisply sorted into each row. When causal conditions are fuzzy sets, however, this analysis is less straightforward because each case may have partial membership in every truth table row … Still, it is important to assess the distribution of cases' membership scores across causal combinations in fuzzy-set analyses because some combinations may be empirically trivial. In other words, if most cases have very low or zero membership in a combination, then it is pointless to assess that combination's link to the outcome. The empirical base for such an assessment would be too weak."
14 We should note that explanatory coverage will differ in the two cases (Ragin 2006b).
15 Since Y + NOT-Y =1, either both Y and NOT-Y are 0.5, or only one of Y and NOT-Y will be above 0.5. It follows from this that the particular paradox we are describing can only arise when X is less than or equal to 0.5. However, not all cases with X =< 0.5 will generate a paradox. Consider the conventional x,y plane. Using the simple fuzzy inclusion rule, we need to have x=< y, for x to be sufficient for y. For x to also be sufficient for not-y, we need x=< (1-y), i.e. y=< 1-x. The region of the plane where these two constraints are met simultaneously is the shaded region plus the boundaries set by y=x and y=1-x. Cases on the line x=0 itself are omitted from calculations of sufficiency in the fsQCA software.
16 If we were to take account of the consistencies for remainder rows, we would, given what we have shown above, be allowing consistencies arising from the paradoxical region of the fuzzy plots in Figures 3 and 4 (and others like these) to play a role in our decisions. On the other hand, if we didn't use these consistencies, we would be open to a charge of ignoring relevant evidence. This paradox-related dilemma is inherent in fuzzy set QCA.
17 Considerable judgement is also required, of course, in using conventional methods.
18 This is something Ragin himself has reflected on, writing in response to a question re this approach: I have thought about this alternate measure of consistency, but not used it for several reasons. The first is that they really are two separate questions: (1) Do I have any real instances of a configuration? (frequency threshold) and (2) Is the evidence consistent with a subset relation (calculation of consistency). On the first question, let's say you have 100 cases and they all have .2 membership in the configuration. These membership scores sum to 20, a substantial number, but you really don't have any instances of the configuration. This justifies the greater than .5 rule. Now the second question. The issue of subsethood really is one about ceilings. The value of Y is a ceiling for the value of X. (IF X exceeds Y by a good margin, then it is evidence against subsethood.) Thus, if X= .4 and Y= .7, this constitutes good evidence in favour of subsethood, even though X is less than .5. (Personal communication to Cooper, 21st June 2004). We should stress that we do not see the alternative approach (i.e. using just good cases) as a panacea for the problems we discussed earlier. Our current view is that it is worth using this in conjunction with the approach embedded in the fsQCA software.
19 Here, Ragin writes in response to Mendel's questions: The point is simply that the parsimonious solution can often be over inclusive with respect to remainders. In fact, it usually is, which is why I almost always favour the intermediate solutions (p. 13). … … The basic idea I've been working with is that parsimonious solutions, in general, cannot be trusted because they incorporate difficult counterfactuals and must therefore be "corrected" via the intermediate solution routine (p. 16.) … … keep in mind that the complex solutions sometimes include what I consider nuisance terms, especially when the diversity of cases is low and the number of causal conditions is great. For example, suppose the outcome is staying out of poverty and one of the conditions included in a successful combination is having "low income parents." If the reason that that this condition is included is simply because there was no matched row with "not-low income parents" (i.e., there were no cases with this specific combination), then having "low income parents" as part of a combination linked to staying out of poverty is truly a nuisance. This is why I almost universally prefer intermediate solutions (p. 35).
20 The aggregating nature of the consistency measure used in the truth table algorithm of fsQCA allows a solution generated using a threshold lower than 1.0 to include, as can be seen here, some "near miss" cases that fall out of the upper triangular area that contains cases satisfying the rule for strict fuzzy sufficiency (i.e. satisfying x= <y). For a rationale for this, see Ragin (2008, pp. 45-54).
21 This table appears to agree with the authors' claim that "child" (i.e. ~CHILD) is necessary for a low degree of inequality, though it should be noted that this conclusion is one based only on the empirically available rows. We can note that, if ~CHILD is quasi-necessary for ~OUTCOME, then CHILD should be quasi-sufficient for OUTCOME. To test the latter claim we need data on all the rows where CHILD=1, but we in fact lack data for four of eight of these.
22 Remainders are all set to false; no counterfactuals (Ragin et al. 2008).
23 Any remainder that will help generate a logically simpler solution is used, regardless of whether it constitutes an "easy" or a "difficult" counterfactual case (Ragin et al. 2008).
24 Only remainders that are "easy" counterfactual cases are allowed to be incorporated into the solution. The designation of "easy" versus "difficult" is based on user-supplied information regarding the connection between each causal condition and the outcome (Ragin et al. 2008).
25 If we generate an intermediate solution here, using all non-zero cases and a threshold of 0.9, and having said that negated conditions should be good for the outcome, we get the same result: child*track.
26 It is also the case that the reasoning used to justify "easy" counterfactuals might be argued to be somewhat non-configurational, since it appears it would be weakened by the existence of any complex interaction effects of which the analyst is ignorant.
27 The conclusions of a paper published by one of us (Cooper 2005a) which was one of the first to use fsQCA to analyse a large dataset, also need to be read with the lessons of this current paper in mind. There was no problem of limited diversity to address, given the size etc. of the dataset. However, the points raised here about the paradoxical region of the x,y plot are relevant. Since that paper was published Ragin has modified the consistency measure in the truth table algorithm. We have run a reanalysis using this new measure, for the outcome, highest level of qualifications achieved, by class, sex and ability. The consistency figures for the outcome are higher with the new measure but the ordering of the rows of the 8-row truth table is identical. The new solution that allows the three rows with the highest consistencies forward (using a threshold of 0.8) reproduces a solution from Cooper (2005a), as does the new four row solution (using a 0.75 threshold). When we look at the solutions for the negated outcome, using these two thresholds, we find just one paradoxical row, this being the row that is in the 0.75 but not the 0.8 solution. This suggests to us that the 3-row solution is more valid. This is borne out by an separate analysis using Ragin's new PRI measure (to remove cases in the inconsistent region of the x,y plot). We find this measure produces lower consistencies. Taking this into account in setting thresholds, we obtain two solutions with no paradoxical rows, one of which is the 3-row solution reported in Cooper (2005a), the other a 2-row solution also reported in that paper. Furthermore, an analysis using just "good" cases, with a threshold of 0.75, produces the same 3-row solution.
References
COOPER, B (2005a) 'Applying Ragin's crisp and fuzzy set QCA to large datasets: social class and educational achievement in the NCDS', Sociological Research Online: <http://www.socresonline.org.uk/10/2/cooper1.html>COOPER, B (2005b) On applying Ragin’s crisp and fuzzy set QCA to large datasets: exploring social class and educational achievement in the National Child Development Study, Methodology stream of European Consortium for Political Research General Conference, Budapest: <http://www.essex.ac.uk/ecpr/events/generalconference/budapest/papers/20/6/cooper.pdf >
COOPER, B and GLAESSER, J (2008a) 'How has educational expansion changed the necessary and sufficient conditions for achieving professional, managerial and technical class positions in Britain? A configurational analysis'. Sociological Research Online: <http://www.socresonline.org.uk/13/3/2.html>
COOPER, B and GLAESSER, J (2008b) 'Exploring configurational causation in large datasets with QCA: possibilities and problems'. ESRC Research Methods Festival. Oxford: <http://www.ncrm.ac.uk/RMF2008/festival/programme/mthd/>
COOPER, B & GLAESSER, J (2010) 'Contrasting variable-analytic and case-based approaches to the analysis of survey datasets: exploring how achievement varies by ability across configurations of social class and sex', Methodological Innovations Online, vol. 5, no. 1 pp. 4-23.
COOPER, B & GLAESSER, J (2011) 'Using case-based approaches to analyse large datasets: a comparison of Ragin's fsQCA and fuzzy cluster analysis', International Journal of Social Research Methodology vol. 14, no. 1 pp. 31-48.
COOPER, B, GLAESSER, J, HAMMERSLEY, M and GOMM, R (in press) Challenging the Qualitative-Quantitative Divide: Explorations in Case-focused Causal Analysis. London & New York: Continuum Press.
COOPER, B and HARRIES, A V (2009) Realistic contexts, mathematics assessment and social class: lessons for assessment policy from an English research programme. In Verschaffel L, Greer B, van Dooren W and Mukhopadhyay S (Eds.) Words and worlds: modelling verbal descriptions of situations. Rotterdam: Sense Publications.
FREITAG, M and SCHLICHT, R (2009) 'Educational Federalism in Germany: Foundations of Social Inequality in Education', Governance: An International Journal of Policy, Administration, and Institutions, vol. 22, no. 1 pp. 47-72.
GLAESSER, J (2008) 'Just how flexible is the German selective secondary school system? A configurational analysis', International Journal of Research and Method in Education, vol. 31, no. 2 pp. 193-209. [doi:://dx.doi.org/10.1080/17437270802212254]
GLAESSER, J and COOPER, B (2010) 'Selectivity and Flexibility in the German Secondary School System: A Configurational Analysis of Recent Data from the German Socio-Economic Panel', European Sociological Review, doi:10.1093/esr/jcq026, available online at <www.esr.oxfordjournals.org>.
GOERTZ, G (2006) 'Assessing the Trivialness, Relevance, and Relative Importance of Necessary or Sufficient Conditions', Studies in Comparative International Development, vol. 41, no. 2 pp. 88-109. [doi:://dx.doi.org/10.1007/BF02686312]
KVIST, J (2007) 'Fuzzy set ideal type analysis', Journal of Business Research vol. 60, pp. 474–481.
MENDEL, J M & RAGIN, C C (2011) fsQCA: Dialog Between Jerry M. Mendel and Charles C. Ragin, USC-SIPI REPORT # 411, <http://www.compasss.org/pages/resources/emailmendel.pdf>, accessed 28/4//11.
RAGIN, C C (1987) The Comparative Method. Berkeley: California University Press.
RAGIN, C C (2000) Fuzzy Set Social Science. Chicago: Chicago University Press.
RAGIN, C C (2005) From Fuzzy Sets to Crisp Truth Tables. <http://www.compasss.org/files/WPfiles/Raginfztt_April05.pdf>, accessed 21st April 2011.
RAGIN, C C (2006a) The limitations of net effects thinking. In B. Rihoux and H. Grimm (Eds.) Innovative Comparative Methods for Political Analysis. New York: Springer.
RAGIN, C C (2006b) 'Set relations in social research: evaluating their consistency and coverage', Political Analysis, vol. 14, no. 3 pp. 291-310. [doi:://dx.doi.org/10.1093/pan/mpj019]
RAGIN, C C (2008) Redesigning Social Inquiry. Chicago: Chicago University Press.
RAGIN, C C, with STRAND, S I & RUBINSON, C (2008) USER'S GUIDE TO Fuzzy-Set / Qualitative Comparative Analysis. Department of Sociology, University of Arizona.
SMITHSON, M J and VERKUILEN, J (2006) Fuzzy Set Theory: Applications in the Social Sciences. Thousand Oaks: Sage.

